Совокупность параметров хj и t называют переменными Эйлера.
Основное различие между методами Лагранжа и Эйлера состоит в том, что с точки зрения Лагранжа нас интересуют законы изменения положения, скорости, ускорения и других величин данной индивидуальной точки сплошной среды, а с точки зрения Эйлера — перемещение, скорость, ускорение и т. д. в точке пространства, мимо которой в данный момент проходят частицы среды.
В механическом отношении оба способа эквивалентны.
При необходимости можно совершить переход от переменных Лагранжа к переменным Эйлера, и наоборот. Если известен закон движения сплошной среды в форме Лагранжа, то, чтобы выразить его в форме Эйлера, достаточно разрешить уравнения (1.1) относительно ξi, т. е. получить
ξi= ξi(x1, x2, x3, t) (1.4)
Эти соотношения при фиксированных координатах хj указывают те точки ξi сплошной среды, которые в разные моменты времени проходят через данную точку пространства.
Если в формулы для проекции скоростей vi= vi(ξ1, ξ2, ξ3, t) и других величин, заданных с точки зрения Лагранжа, подставить соотношения (1.4), то будут найдены функции в переменных Эйлера хj и t.
В том случае, когда задано распределение скорости в форме Эйлера (1.3), учитывая равенства (1.2), получим систему обыкновенных дифференциальных уравнений относительно хi:
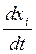= vi(x1, x2, x3, t) (i = 1, 2, 3).
Решив эту систему, найдем xj = xj(C1, C2, C3, t), где С1, С2, С3 — постоянные, определяемые по хj, при t = t0 , т. е. они являются координатами индивидуальной точки сплошной среды (переменными Лагранжа).
Если распределение плотности задано с точки зрения Лагранжа ρ = ρ (ξ1, ξ2, ξ3, t), то определить изменение плотности частицы сплошной среды очень просто, оно равно (dρ/dt)ξi. Сложнее, когда ρ = ρ(xl, x2, x3, t), т.е. функция задана в переменных Эйлера. В этом случае необходимо перейти от переменных Эйлера к переменным Лагранжа и воспользоваться правилом дифференцирования сложной функции, что приведет к формуле
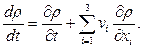(1.5)
Производная dρ/dt характеризует изменение плотности данной частицы сплошной среды в единицу времени и называется индивидуальной, субстанциональнойили полнойпроизводной. Производная ∂ρ/∂t характеризует изменение плотности в данной точке пространства в единицу времени и называется местной или локальной.
Сумма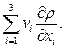 
— в правой части (1.5) называется конвективной производной.
Аналогично формуле (1.5) можно написать формулы для определения полной производной по времени проекций любой векторной величины, заданной в переменных Эйлера.
Например, ускорение частицы сплошной среды в проекциях на оси декартовой системы координат имеет вид
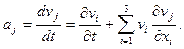(j = 1, 2, 3) (1.6)
Дата добавления: 2015-03-07; просмотров: 1177;