Роль науки о механике сплошной среды 23 страница
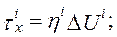
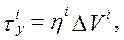
где ti, - касательные напряжения в связях сдвига i-го шва; hi - коэффициент жесткости связей сдвига i-го шва; DUi, DVi - разность продольных перемещений в направлениях x и у соответственно.
Качество крепления скважин всегда было и остается до настоящего времени актуальной задачей механики сплошных сред для всех нефтедобывающих предприятий, решение которой не терпит отлагательств. Основные усилия зарубежных исследователей в настоящее время направлены на создание цифровых моделей крепи скважины, учитывающих влияние профиля скважины, гидравлических сопротивлений, перфорации и т.д. При этом учитывая большую сложность создаваемых моделей, исследования в основным направлены на повышение эффективности их работы, но результаты расчетов по ним пока не известны.
Для повышения герметичности крепи скважин, подвергающейся действию динамических нагрузок, наиболее целесообразно усилить сцепляемость цементного камня и стальной поверхности обсадной трубы, создавая на её поверхности шероховатый слой для армирования, при котором цементная матрица увеличивает возможность воспринимать усилия любой направленности, предупреждая образование и развитие трещин в цементном камне.
В настоящее время при применении численных методов возникает вопрос устойчивости численного процесса. В случае, если точность решения вызывает сомнение необходимо сделать оценку условий сходимости решения.
Вопрос устойчивости решения является особенно актуальным при решении задач изгиба составных пластин и оболочек, когда количество разрешающих уравнений зависит от количества слоёв и количества швов. К решению задач изгиба применительно к составным оболочкам разработан метод, основанный на схеме Зейделя (метод последовательных приближений) с решением относительно искомых параметров по блокам.
Из краткого обзора методов расчёта изгиба слоистых пластин и оболочек следует отметить, что каждый из существующих методов применим для своего определённого круга задач. Метод конечных элементов(МКЭ) является наиболее универсальным. Определённые математические трудности представляет решение задач изгиба составных пластин и пологих оболочек с переменной жёсткостью и учётом сдвига между слоями.
В соответствии с проведенным анализом работ, где рассматриваются вопросы прочности крепи скважин и методы их расчета, сформулированы следующие задачи механики сплошных сред в бурении и разработке нефтяных и газовых месторождений:
1. Комплексное изучение состояния крепи скважин на месторождениях в районах вечной мерзлоты Западной Сибири.
2. Анализ имеющихся методик расчета крепи скважин от воздействия наружных давлений.
3. Разработка и уточнение методов расчета, и обоснование выбора типа материала, толщины стенок обсадных труб, физико-механических свойств тампонажного камня с учетом их устойчивости к воздействию локальных осесимметричных нагрузок.
4. Разработка технических и технологических рекомендаций по повышению прочности крепи скважин к воздействию избыточных внешних давлений.
5. Анализ воздействия наружных давлений горных пород в зоне пластичных и текучих кошайских глин, а также поведение системы «скважина-пласт» в интервалах люлинворской свиты.
6. Анализ фильтрационных свойств продуктивных пластов для повышении дебита при уменьшении влияния Скин-эффекта призабойной зоны при горизонтальном бурении.
§ 1. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Общая задача кинематики — описание движения среды безотносительно к тому, какие внешние условия вызывают и поддерживают данное движение.
Так как сплошная среда представляет собой непрерывную совокупность точек, то определить движение среды — значит описать движение всех ее точек.
Движение всегда определяется по отношению к некоторой системе отсчета - системе координат. Условимся через x1, х2, х3 обозначать координаты любой ортогональной системы координат, если нет специальной оговорки.
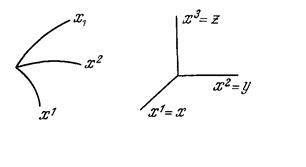
Рис. 1
Существуют два исторически сложившихся способа задания движения. Первый из них, связанный с именем Лагранжа, заключается в задании кинематических уравнений движения:
xi= xi (ξ1, ξ2, ξ3, t) (i = 1. 2, 3), (1.1)
где ξi - являются координатами фиксированной (или индивидуальной) точки среды. Совокупность величин ξi и t называют переменными Лагранжа.
Основная задача механики сплошной среды заключается в определении закона движения (1.1). Построение математической модели любой сплошной среды явно или неявно опирается на понятие закона движения.
При лагранжевом задании движения проекции скоростей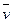 
и ускорений 
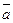точек среды на оси координат хi, определяются обычными равенствами
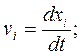
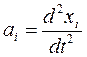. (1.2)
Хотя лагранжев способ и применяется в некоторых задачах механики сплошных сред, все же он уступает другому, более широко используемому способу Эйлера, который заключается в задании перемещений и, скоростей v, ускорений а и других интересующих нас величин как функций координат точек пространства хi и времени t, т. е.
ui = ui(x1, x2, x3, t);
vi = vi(x1, x2, x3, t);
ai = ai(x1, x2, x3, t).(1.3)
Дата добавления: 2015-03-07; просмотров: 921;