Система плоских прямоугольных координат
Для решения практических задач применяется более простая и удобная прямоугольная система координат на плоскости – система Декартовых координат. В этой системе начальными являются две взаимно перпендикулярные линии на горизонтальной плоскости, служащие осями системы. Точка О пересечения координатных осей X и Y является началом координат. В геодезии, в отличие от математики, ось абсцисс совмещают с каким-либо меридианом, поэтому положительное направление оси Х на север (вверх листа), а оси Y на восток (вправо). Оси координат образуют координатные четверти, которые обозначают римскими цифрами и нумеруют по часовой стрелке, первой считается северо-восточная четверть. Названия четвертей соответствуют сторонам света: I – СВ, II – ЮВ, III – ЮЗ, IѴ - СЗ. Положение точки определяется координатами х и у - расстояниями от начала координат до проекций точки на координатные оси. Знаки координат плюс (+) или минус (-) зависят от четверти, в которой находится точка (рис.1.5).
|
|

Рис.1.5. Прямоугольная система координат
Иногда ось Х удобно не совмещать с направлением меридиана, а выбирать произвольно, дать ей другое более выгодное направление. Такая система называется условной или местной системой прямоугольных координат. Условная система применяется на строительных площадках, при шахтном строительстве и т.п.
 4.3.Приращения координат
4.3.Приращения координат
Приращением координат называется разность координат двух точек, обозначается буквой D с добавлением названия оси, получается вычитанием из координат конечной точки отрезка координат начальной точки его : Dx = x кон - xнач ; Dy = y кон - y нач .
Если известны координаты начальной точки отрезка и приращения координат, то можно вычислить координаты конца отрезка
хкон = хнач + Dх ; y = у нач + Dу, с учетом знака приращения .
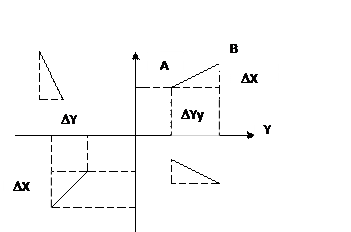
Рис.1.6. Приращения координат
 В географической системе: Dj =j2-j1; Dl = l 2 -l 1; j2 =j1 +Dj ; l2=l1 +D l. Приращения координат используются при решении геодезических задач, например, для вычислении длины отрезка d = √DХ2 + DY2 .
В географической системе: Dj =j2-j1; Dl = l 2 -l 1; j2 =j1 +Dj ; l2=l1 +D l. Приращения координат используются при решении геодезических задач, например, для вычислении длины отрезка d = √DХ2 + DY2 .
Дата добавления: 2015-03-19; просмотров: 3287;
