Сведения о фигуре и размерах Земли

Одной из задач геодезии является определение фигуры и размеров Земли. Из истории человечества известно, что с. ѴΙ до н.э. (Пифагор) и до конца ХѴΙΙв. Землю принимали за шар. В дальнейшем ученые (Ньютон) уточнили, что Земля сплюснута у полюсов и считали ее сфероидом близким к эллипсоиду вращения. При определении фигуры и размеров Земли в геодезии исходят из понятия уровенных поверхностей. Уровенной называют поверхность, которую направление отвесной линии пересекает под прямым углом. Отвесной линиейназывают линию, совпадающую с направлением силы тяжести.

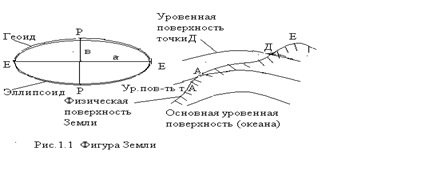
Большую часть поверхности Земли (71%) занимает океан. Поверхность воды в нем под действием силы тяжести в каждой точке перпендикулярна направлению силы тяжести, следовательно, является уровенной поверхностью и всюду горизонтальна. Уровенную поверхность воды в океанах и сообщающихся с ними морях в их спокойном состоянии (без волн, приливов и течений) мысленно продолженную под материками так, чтобы она в каждой точке пересекала направление отвесной линии под прямым углом, называют основной уровенной поверхностьюили уровнем океана. Фигуру, образованную основной уровенной поверхностью, принимают за сглаженную фигуру Земли и называют геоидом (фигура подобная Земле). ( Название предложил в 1783г. немецкий физик Листинг из Гёттингена).

При детальных исследованиях установили, что вследствие неодинаковой плотности масс внутри Земли, геоид представляет собой поверхность с изменяющейся кривизной, то есть имеет неправильную геометрическую форму и не поддается математическому представлению. Для геодезических вычислений нужна фигура наиболее приближенная к геоиду и описываемая математическими выражениями. Ближе всего к поверхности геоида подходит правильная геометрическая фигура – эллипсоид вращения, получаемая вращением эллипса вокруг малой оси, которая называется общеземным эллипсоидом. Его принимают за математическую фигуру Земли.

Отвесная линия и уровенная поверхность в геодезии имеют важное значение, они служат начальными при геодезических измерениях.

Размерами эллипсоида являются большая полуось а, малая полуось в и полярное сжатие a, равное отношению разности полуосей к большой полуоси a =(а - в) : а.

Первое определение размеров Земли выполнил в IIIв. до н.э. Эратосфен. Размеры земного эллипсоида в разные годы более точно определили в 19в.ученые многих стран: Деламбр, Франция, 1800г.; Бессель, Германия, 1841; Кларк, Англия, 1880; Жданов, Россия, 1893; Хейфорд, США, 1909; Красовский, СССР,1940.

Поверхности геоида и эллипсоида не совпадают, поэтому земной эллипсоид мысленно ориентируют, т.е. располагают в теле Земли так, чтобы отклонения его от поверхности геоида были минимальными в пределах отдельной страны. Земной эллипсоид с известными размерами и ориентированный в теле Земли для данной страны или части Земли называется референц-эллипсоидом. В каждой стране принят свой референц-эллипсоид. В нашей стране с 1946 г. применяется референц-эллипсоид Красовского, размеры которого вычислены под руководством выдающегося российского геодезиста Красовского Ф.Н., с размерами: а = 6378245м, в = 6356863м; a = 1: 298,3. Его поверхность принята совпадающей с поверхностью геоида в Кронштадте. (До него в России применяли эллипсоид Бесселя).

Отклонения поверхности геоида от эллипсоида невелики (на равнине 0,1 – 0,2м, в горах – до 2м.) Поэтому, в инженерной геодезии и топографии поверхности геоида и эллипсоида считают совпадающими. Во многих случаях незначительные по размерам участки земной поверхности площадью до 400км² (квадрат со стороной 20км или окружность радиусом 10км) принимают за плоскость. При необходимости учета сферичности Земли ее считают шаром, объем которого равен объему земного эллипсоида. Радиус R такого шара равен 6371км.

.

С помощью искусственных спутников Земли были уточнены размеры эллипсоида и в настоящее время в качестве международной принята геодезическая референцная система параметров Земли ПЗ – 90, в которой а = 6378136м; a = 1: 298, 3932578.