Сложное колебание и его гармонический спектр

Как видно из § 5.3, сложение колебаний приводит к более сложным формам колебаний. Для практических целей бывает не­обходимой противоположная операция: разложение сложного ко­лебания на простые, обычно гармонические, колебания.

Ж. Фурье показал, что периодическая функция любой сложнос­ти может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции.

Такое разложение периодической функции на гармонические Составляющие и, следовательно, разложение различных периоди­ческих процессов (механические, электрические и т. п.) на гармо­нические колебания называется гармоническим анализом. Су­ществуют математические выражения, которые позволяют найти составляющие гармонические функции. Автоматически гармони­ческий анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами — анализаторами.

Совокупность гармонических колебаний, на которые разложе­но сложное колебание, называется гармоническим спектром сложного колебания.

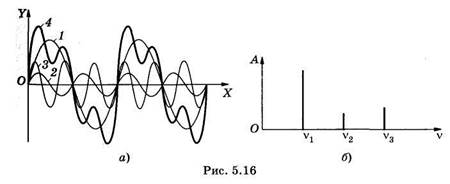
Гармонический спектр удобно представить как набор частот (или круговых частот) отдельных гармоник совместно с соответст­вующими им амплитудами. Наиболее наглядно такое представле­ние выполняется графически. В качестве примера на рис. 5.16, а изображены графики сложного колебания (кривая 4) и составляю­щих его гармонических колебаний (кривые 1, 2 и 3); на рис. 5.16, б показан гармонический спектр, соответствующий этому примеру.

Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс, он находит применение в акустике, радиотехнике, электронике и других областях науки и техники.