Вращательные спектры.

Вращательную энергию молекул обычно рассматривают на основании модели жёсткого ротатора, который представляет собой два атома, находящиеся один от другого на строго фиксированном расстоянии. Для того чтобы получить уравнение для расчёта энергетических состояний вращательного движения такой системы связанных между собой атомов, необходимо записать и решить стационарное волновое уравнение Шрёдингера:

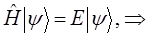
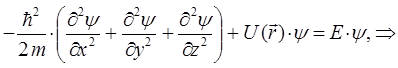
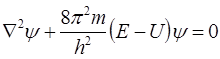
Поскольку для системы жёсткого ротатора потенциальная энергия есть величина постоянная (расстояние между ядрами в молекуле - постоянная величина), тогда:

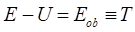
здесь 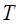-кинетическая энергия ротатора. Таким образом, для молекулы типа жёсткого ротатора необходимо решить уравнение вида:

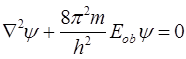
Наиболее интересным результатом решения такого волнового уравнения является установление простой взаимосвязи вращательной энергии молекулы и некоторым числом 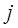, которое может принимать все значения целых положительных чисел, начиная с нуля:

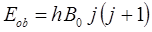
где

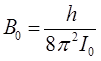
является величиной постоянной и называется вращательной постоянной. Выражение для энергии вращательных состояний двухатомной молекулы можно также получить и, не решая уравнение:

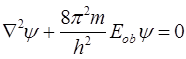
если основываться только на общих свойствах векторов момента количества движения (углового момента) в квантовой и классической механике.

Так, момент количества движения (углового момента) в квантовой механике определяется выражением вида:

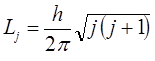
с другой стороны, согласно классической теории имеем для двухатомной молекулы:

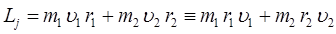
с учётом выражения вида:

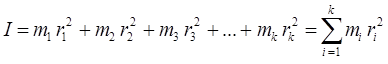
или для системы жёсткого ротатора:

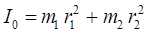
Полученное выражение для момента инерции жёсткого ротатора можно видоизменить, введя в данное уравнение так называемую приведенную массу:

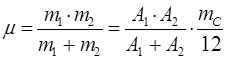
где A_i - атомные массы атомов, входящих в состав молекулы; m_C - масса атома углерода и 12 - относительная атомная масса изотопа углерода С¹², тогда:

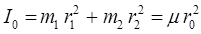
Учитывая также выражение, связывающее линейные скорости движения атомов в двухатомной молекуле с циклической частотой:

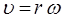
или для случая жёсткого ротатора:

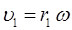
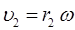
будем иметь соответственно для классического выражения момента количества движения (углового момента):

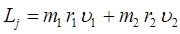
откуда следует соответственно:

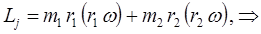
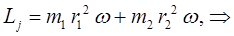
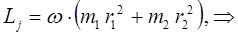
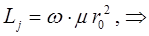
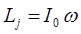
откуда соответственно следует, что:

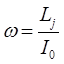
учитывая выражение для углового момента, его квантово-механическую трактовку:

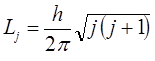
будем иметь:

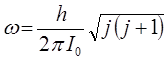
На основании выражения вида:

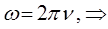
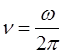
несложно записать соответствующие уравнения для линейной частоты:

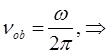
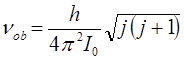
Энергия вращательного движения ротатора определяется выражением вида:

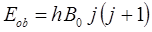
где

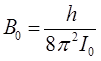
или после соответствующей подстановки:

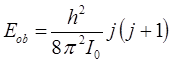
Таким образом, молекула может вращаться лишь с определёнными частотами, т.е. она владеет набором дискретных вращательных уровней энергии.

Уравнение вида:

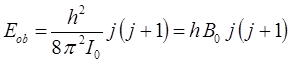
даёт следующие дискретные значения вращательной энергии молекулы:

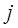
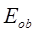
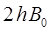
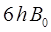
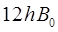
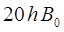
Число 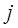называется орбитальным квантовым числом. Оно определяет величину вращательной энергии молекулы в данном её энергетическом состоянии. Таким образом, для молекулы возможна серия дискретных вращательных энергетических уровней, энергия которых возрастает прямо пропорционально (линейно) квадрату вращательного квантового числа 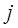. При этом каждому энергетическому уровню отвечает значение вращательного терма, которое определяется на основании выражения вида:

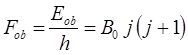
При переходах молекулы из одного энергетического состояния в другое, между вращательными подуровнями основного электронного и нулевого колебательного состояний возникает вращательный спектр. Если молекула переходит от вращения, что характеризуется квантовым числом 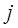, к вращению с квантовым числом 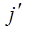, то испускается квант энергии:

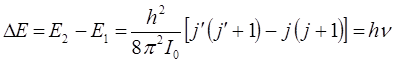
на основании правила отбора Паули, разница квантовых чисел может равняться:

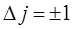
при поглощении кванта энергии:

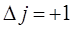
при излучении кванта энергии:

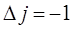
Разница энергий двух уровней, для которых вращательное квантовое число отличается на единицу, т.е. когда:

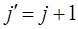
составляет:

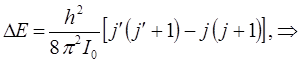
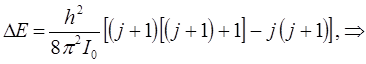
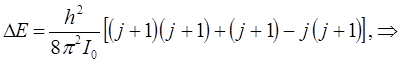
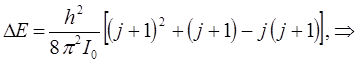
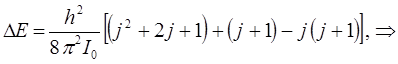
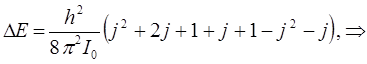
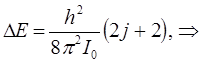
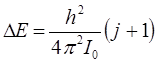
Если же 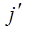отвечает более высокому энергетическому состоянию, чем 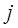, то не сложно получить выражение для расчётов частоты линии во вращательном спектре как функцию вращательного квантового числа 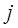низшего из состояний. Имеем соответственно:

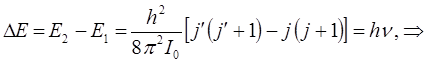
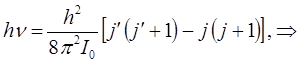
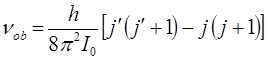
или с учётом того, что:

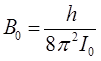
будем иметь соответственно:

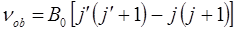
Поскольку:

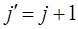
имеем:

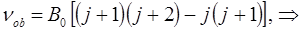
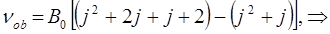
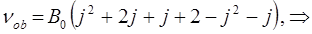
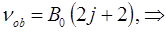
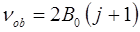
Очевидно расстояние между любыми линиями во вращательном спектре, выраженная в частотах, будет равняться некоторой постоянной величине:

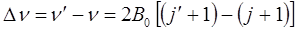
поскольку:

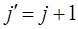
тогда соответственно:

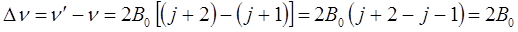
Как это видно из полученного выражения, вращательный спектр двухатомной молекулы представляет собой серию равноотстоящих линий, отвечающих различным значениям вращательного квантового числа 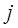(так называемый эквидистантный спектр). Однако в области больших частот постепенно уменьшается расстояние между спектральными линиями за счёт не жёсткости молекулы, а это в свою очередь означает, что вращательная энергия зависит также и от потенциальной энергии. Определив расстояние между соседними линиями вращательного спектра, можно найти вращательную постоянную. При этом зачастую, становится удобным связать расстояние между линиями вращательного спектра с моментом инерции. Так, имеем:

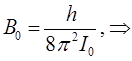
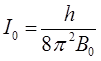
учитывая, что:

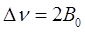
откуда после несложных преобразований находим:

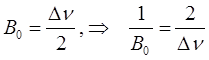
имеем соответственно:

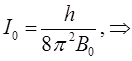
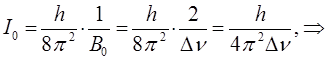
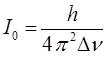
Учитывая известные соотношения:

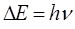
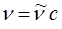
откуда следует:

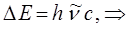
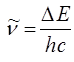
а также учитывая полученное нами уже ранее выражение для энергии:

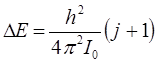
несложно получить для волнового числа 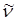уравнение вида:

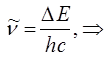
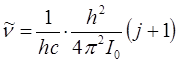
и таким образом имеем:

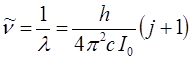
Как уже оговаривалось выше, в реальной молекуле вращательная энергия зависит также от потенциальной энергии:

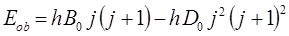
а расстояние между соответствующими энергетическими уровнями:

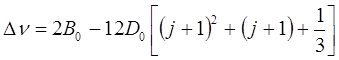
Вращательный спектр поглощения наблюдается только у соединений, которые находятся в газообразном состоянии. Это объясняется тем, что энергия межмолекулярных взаимодействий между молекулами в жидком и твёрдом состояниях вещества превышает энергию вращения. Чисто вращательные спектры наблюдаются в микроволновой и дальней инфракрасной областях. Энергия квантов в этой области спектра равна порядка 1,2 кДж/моль и меньше. Это значение соизмеримо с энергией теплового движения kT, поэтому уже при комнатной температуре часть вращательных уровней заселена. В настоящее время чисто вращательные спектры в аналитических целях почти не используют. Их применяют главным образом для исследования строения молекул, определения межъядерных расстояний и т.д.