Колебательные спектры. 2 страница
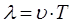
учитывая, что:
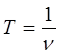
будем иметь соответственно:
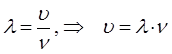
Две волны называют когерентными, если частицы колеблются в одинаковых фазах. Геометрическое место точек, до которых доходят колебания к моменту времени 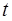 , называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. Если волновая поверхность представляет собой совокупность плоскостей, параллельных друг другу, то такая волна называется плоской. Если же волновая поверхность представляет совокупность концентрических сфер, параллельных друг другу, то такая волна будет называться сферической. Пусть в системе происходит волновой процесс и в точке
, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. Если волновая поверхность представляет собой совокупность плоскостей, параллельных друг другу, то такая волна называется плоской. Если же волновая поверхность представляет совокупность концентрических сфер, параллельных друг другу, то такая волна будет называться сферической. Пусть в системе происходит волновой процесс и в точке 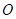 находится начальная фаза колебаний
находится начальная фаза колебаний 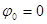 (примем, что оно совершается по закону синуса). Для упрощения выкладок будем рассматривать плоскую волну, распространяющуюся вдоль одной из координатных осей (например, вдоль оси
(примем, что оно совершается по закону синуса). Для упрощения выкладок будем рассматривать плоскую волну, распространяющуюся вдоль одной из координатных осей (например, вдоль оси 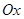 ) – одномерный случай, тогда будем иметь соответственно:
) – одномерный случай, тогда будем иметь соответственно:
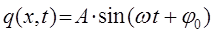
после подстановки начального условия 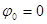 , будем иметь:
, будем иметь:
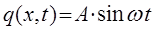
Возьмём на прямой 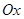 произвольную точку М, лежащую от начала координат (точка
произвольную точку М, лежащую от начала координат (точка 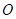 ) на расстоянии
) на расстоянии 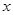 . Очевидно, что колебания распространяясь от точки
. Очевидно, что колебания распространяясь от точки 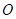 , дойдут до точки М через промежуток времени
, дойдут до точки М через промежуток времени 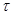 . Тогда, следовательно:
. Тогда, следовательно:
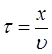
Таким образом, точка М начнёт колебаться на время 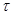 позже точки
позже точки 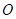 , поэтому:
, поэтому:

или с учётом соотношения вида:
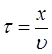
получим соответственно:
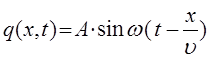
Полученное выше соотношение, представляет собой уравнение плоской волны, распространяющейся вдоль оси 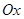 . Фронт такой волны будет представлять собой плоскость. Данное уравнение задаёт смещением
. Фронт такой волны будет представлять собой плоскость. Данное уравнение задаёт смещением 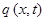 как функцию времени
как функцию времени  и расстояния
и расстояния 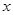 от точки М до центра колебаний лежащего в точке
от точки М до центра колебаний лежащего в точке 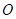 .
.
Очевидно, что аргумент:
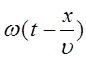
есть не что иное как фаза волны 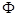 . Если представить себе волну, распространяющуюся в направлении, обратном рассмотренному выше, тогда уравнение плоской бегущей волны вида:
. Если представить себе волну, распространяющуюся в направлении, обратном рассмотренному выше, тогда уравнение плоской бегущей волны вида:
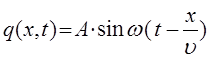
должно быть заменено уравнением вида:

Полученные нами выше уравнения для двух взаимообратных плоских бегущих волн:
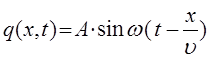

могут быть преобразованы далее к виду:
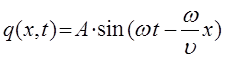
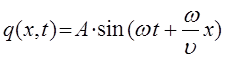
учитывая выражения вида:
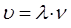
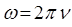
будем иметь соответственно:

здесь величина вида:

представляет собой волновой вектор. Тогда соответствующие уравнения для плоских бегущих волн можно представить к виду:
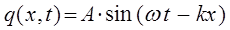
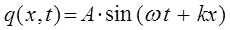
Для последующих выкладок удобней представить полученные выражения в экспоненциальной форме. При этом ограничимся рассмотрением лишь таких волн, которые распространяются вдоль оси 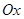 в прямом направлении.
в прямом направлении.
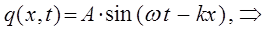
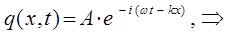

Уравнение де Бройля (для случая плоских волн), есть одно из возможных решений дифференциального уравнения в частных производных, описывающее процесс распространения возмущения (колебания) в среде. Такое уравнение называется волновым уравнением. Для его получения необходимо дважды продифференцировать полученное выше уравнение плоской бегущей волны по координате 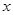 и дважды по времени
и дважды по времени  .Имеем соответственно:
.Имеем соответственно:
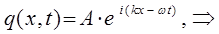
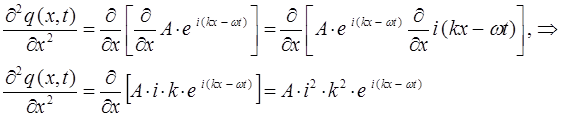
с учётом выражений вида:
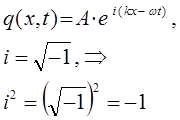
будем иметь соответственно:
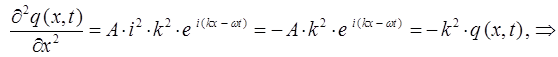
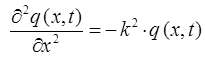
Аналогично получаем значение второй производной по времени:
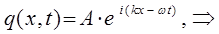
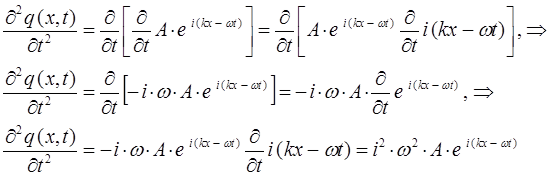
с учётом выражений вида:
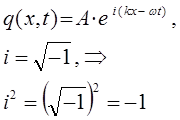
будем иметь соответственно:
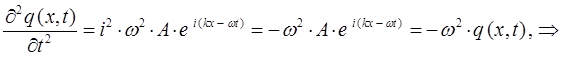

Таким образом, в ходе проделанных операций дифференцирования, мы пришли к выражениям вида:


Выражая из полученных выражений величину  и приравнивая между собой общую переменную
и приравнивая между собой общую переменную  , будем иметь соответственно:
, будем иметь соответственно:
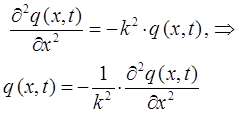
аналогично:
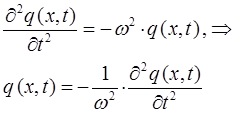
имеем таким образом:
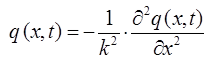
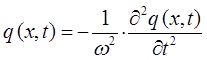
откуда следует, что:
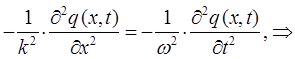
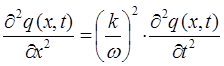
с учётом выражения вида:
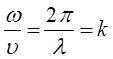
будем иметь соответственно:
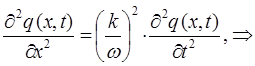
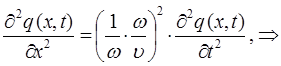
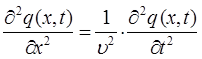
для случая электромагнитных волн, имеем:
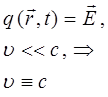
тогда соответственно:
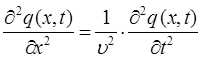
Полученное нами выше волновое уравнение описывает распространение плоской бегущей электромагнитной волны вдоль оси  . Однако оно остаётся справедливым и для трёхмерного случая. Распространяя данное уравнение для случая трёх пространственных координат, полученное выше волновое уравнение можно записать в обобщённом виде:
. Однако оно остаётся справедливым и для трёхмерного случая. Распространяя данное уравнение для случая трёх пространственных координат, полученное выше волновое уравнение можно записать в обобщённом виде:
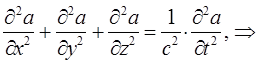
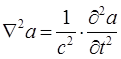
Так, одной из основных задач классической механики является нахождение траектории движения частицы (или системы частиц). Для этого необходимо составить и решить уравнение движения и получить зависимость координат от времени. Зная координаты частицы в настоящий момент времени, можно предсказать её положение в любой последующий момент времени. В отличие от классической, квантовая механика включает в себя совершенно новую концепцию движения. В соответствии с принципом неопределённости Гейзенберга, для квантово-механической системы нельзя рассчитать траекторию движения. Следовательно, для описания движения не по траекториям квантовая механика должна использовать новые понятия и представления. Центральным понятием квантовой механики является волновая функция  , которая по аналогии с гармоническими колебаниями и волнами характеризует амплитуду (распределение) стоячих волн в пространстве. Данное понятие было введено в квантовую механику Э. Шрёдингером. Волновая функция зависит от координат
, которая по аналогии с гармоническими колебаниями и волнами характеризует амплитуду (распределение) стоячих волн в пространстве. Данное понятие было введено в квантовую механику Э. Шрёдингером. Волновая функция зависит от координат 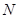 частиц, т.е. от радиус-векторов
частиц, т.е. от радиус-векторов 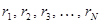 и в общем случае от времени
и в общем случае от времени 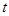 и обозначается
и обозначается 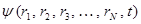 , тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме:
, тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме:
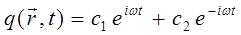
может быть записано в виде:
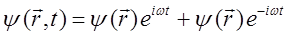
где выражения:
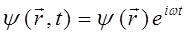
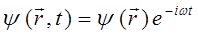
частные решения соответствующего дифференциального уравнения. Необходимо отметить, что одно из частных решений будет комплексно сопряжённым другому. При этом суперпозиция соответствующих частных решений, образуют стоячую волну, состоящую из двух бегущих волн.
Поскольку волновая функция 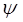 - комплексная величина, т.е.
- комплексная величина, т.е.
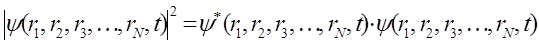
то физический смысл будет иметь не сама волновая функция 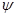 , а квадрат её модуля
, а квадрат её модуля 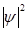 . По аналогии со световыми волнами, квадрат амплитуды
. По аналогии со световыми волнами, квадрат амплитуды 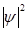 пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или
пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или 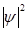 определяет число частиц в единице объёма. Если рассматривать единичную частицу, то квадрат амплитуды
определяет число частиц в единице объёма. Если рассматривать единичную частицу, то квадрат амплитуды 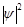 даёт вероятность нахождения частицы в единице объёма или плотность вероятности:
даёт вероятность нахождения частицы в единице объёма или плотность вероятности:
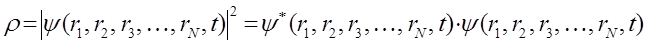
Очевидно, произведение плотности вероятности 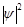 на элементарный объём
на элементарный объём 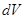 - есть вероятность нахождения частицы в элементарном объёме, т.е. в области с координатами
- есть вероятность нахождения частицы в элементарном объёме, т.е. в области с координатами 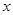 и
и 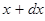 ,
, 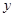 и
и 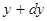 ,
, 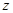 и
и 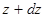 . Таким образом, амплитуда волны де Бройля получает статистическое истолкование, а для единичной частицы – вероятностное толкование. Квадрат амплитуды волны де Бройля
. Таким образом, амплитуда волны де Бройля получает статистическое истолкование, а для единичной частицы – вероятностное толкование. Квадрат амплитуды волны де Бройля 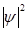 равен вероятности нахождения частицы в единице объёма, её плотности вероятности. Аналитически данное положение, являющееся одним из постулатов квантовой механики, задаётся выражением вида:
равен вероятности нахождения частицы в единице объёма, её плотности вероятности. Аналитически данное положение, являющееся одним из постулатов квантовой механики, задаётся выражением вида:
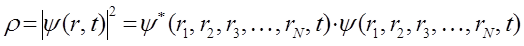
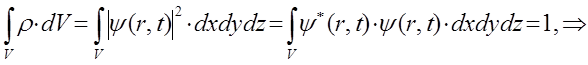
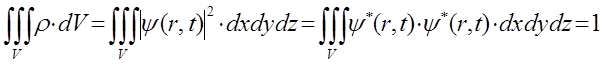
Этот постулат был выдвинут впервые М. Борном. Волны де Бройля – это волны вероятности, они не материальны, т.е. не связаны с каким-либо переносом энергии. Отсюда становится понятным, почему при рассмотрении волнового процесса, в качестве модели выбирают так называемые стоячие волны, распространение которых не связано с переносом энергии и потому являющиеся стабильными, постоянными во времени. Итак, в квантовой механике описание состояния частицы (или системы частиц) выполняется с помощью волновой функции 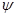 , которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация
, которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация 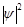 как вероятности нахождения частицы в элементе объёма
как вероятности нахождения частицы в элементе объёма 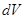 , находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, найдём изначально стационарные решения волнового уравнения, строго зависящие от частоты
, находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, найдём изначально стационарные решения волнового уравнения, строго зависящие от частоты 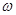 , имеем соответственно:
, имеем соответственно:
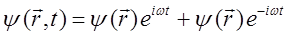
При этом получаемые решения должны удовлетворять требованиям регулярности и граничному условию. К требованиям регулярности относят: конечность, однозначность, и непрерывность волновой функции. Требование конечности означает, что величины 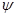 и
и 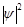 не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме
не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме 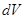 - всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции
- всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции 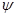 означает, что нет такого элементарного объёма
означает, что нет такого элементарного объёма 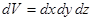 , где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции
, где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции 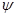 в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции
в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции 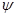 можно записать, через символ Кронекера:
можно записать, через символ Кронекера:
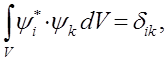
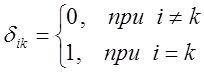
Основываясь на хорошо известной из математики теореме о полной вероятности, можно утверждать, что вероятность обнаружить частицу во всём объёме равна сумме вероятностей во всех точках этого пространства и равна единице:
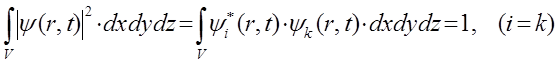
Таким образом, условие нормировки является следствием этой математической теоремы. Действительно, если электрон находится в некотором объёме 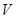 и известна волновая функция электрона
и известна волновая функция электрона 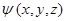 . Тогда при разбиении объёма
. Тогда при разбиении объёма 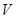 на бесконечно малое число элементарных объёмов
на бесконечно малое число элементарных объёмов 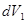 ,
, 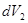 ,
, 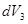 , …,
, …, 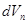 , вероятность обнаружить электрон в каждом из элементарных объёмов будет очевидно определяться выражениями вида:
, вероятность обнаружить электрон в каждом из элементарных объёмов будет очевидно определяться выражениями вида:
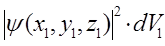


.……………………….
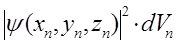
Поскольку вероятность достоверного события равна единице, то очевидно полная вероятность (вероятность нахождения электрона во всём объёме 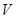 ) равна сумме вероятностей отдельных событий и равна единице:
) равна сумме вероятностей отдельных событий и равна единице:
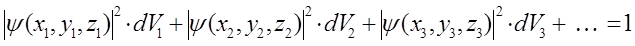
Переходя к бесконечно малым элементам объёма, суммирование можно заменить интегралом вида:

Из условия нормировки также следует, что волны вероятности 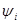 и
и 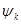 соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме
соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме 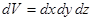 всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:
всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:
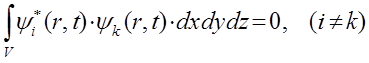
откуда следует, что волны вероятности 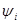 и
и 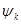 соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Поскольку по определению волновая функция
соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Поскольку по определению волновая функция 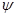 должна быть конечной, т.е. величины
должна быть конечной, т.е. величины 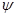 и
и 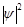 не могут принимать бесконечно большие значения, тогда в соответствии с принципом конечности, стационарное (не зависящее от времени), решение выбираем в виде:
не могут принимать бесконечно большие значения, тогда в соответствии с принципом конечности, стационарное (не зависящее от времени), решение выбираем в виде:
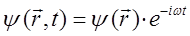
Рассматривая для простоты выкладок одномерный случай, будем иметь соответственно:
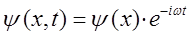
Легко показать, что выбранное в соответствии с описанными выше физически осмысленными условиями решение, соответствует уравнению плоской волны де Бройля, имеющей вид:
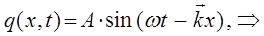
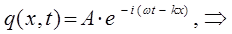
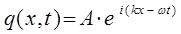
Учитывая, что величине смещения  , амплитуды волны в квантовой механике соответствует волновая функция
, амплитуды волны в квантовой механике соответствует волновая функция 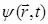 , тогда соответственно будем иметь:
, тогда соответственно будем иметь:

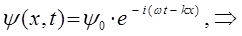
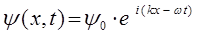
Из полученного уравнения достаточно хорошо видно, что волновая функция 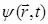 есть произведение координатной волновой функции на член, выражающий зависимость её от времени, т.е.
есть произведение координатной волновой функции на член, выражающий зависимость её от времени, т.е.
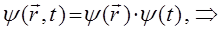
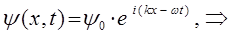

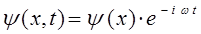
Для получения нестационарного уравнения Шрёдингера, необходимо преобразовать выражение:

к виду, используя соответствие между импульсом и волновым вектором, энергией и циклической (круговой) частотой.
Имеем таким образом:
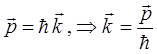
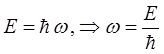
тогда соответствующее выражение для плоской волны де Бройля, с учётом этих условий, после подстановки значений 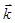 и
и 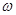 , перепишется в виде:
, перепишется в виде:
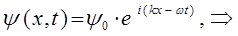
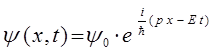
Поскольку гамильтониан есть дифференциальный оператор, то очевидно для нестационарных процессов, его действие при решении задачи на собственные значения оператора будет сводиться к нахождению частной производной по времени от функции 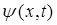 :
:
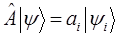
Учитывая, что значение амплитуды волны де Бройля 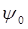 будет находиться и в правой, и в левой частях тождества и как следствие сократится, имеем соответственно:
будет находиться и в правой, и в левой частях тождества и как следствие сократится, имеем соответственно:

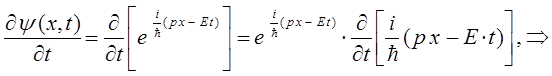

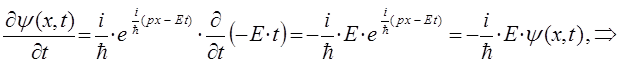
поскольку:
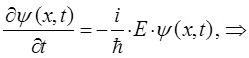
тогда:
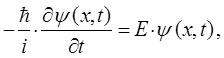
учитывая, что:
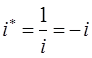
будем иметь соответственно:
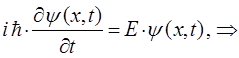
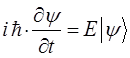
постоянство энергии 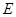 позволяет сделать замену вида:
позволяет сделать замену вида:
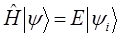
тогда соответственно:
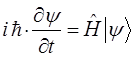
Таким образом, в ходе проделанных выкладок приходим к двум эквивалентным друг другу уравнениям:
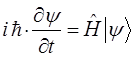
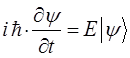
Полученные уравнения справедливы для произвольного гамильтониана, допускающего явную зависимость от времени. Уравнение Шрёдингера как линейное дифференциальное уравнение второго порядка в частных производных, имеет бесчисленное множество решений. Из них интерес представляют лишь такие, которые удовлетворяют требованиям регулярности и граничному условию. В обычных задачах квантовой химии при интерпретации свойств и структуры молекул, как правило, важны стационарные (не зависящие от времени) состояния. В стационарных состояниях плотность вероятности, электронная плотность, а также и другие физические величины не зависят от времени. Можно показать, что нестационарное уравнение Шрёдингера:
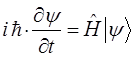
сводится к стационарному (не зависящему от времени) уравнению Шрёдингера. Для этого запишем волновую функцию для электрона, находящегося в стационарном состоянии:
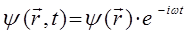
учитывая условия вида:
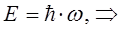
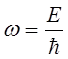
будем иметь соответственно:
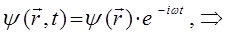
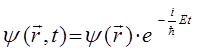
Подставляя данное выражение в нестационарное уравнение Шрёдингера:
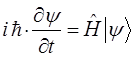
будем иметь соответственно:
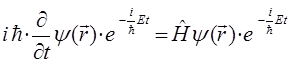
Продифференцируем левую часть данного операторного уравнения:
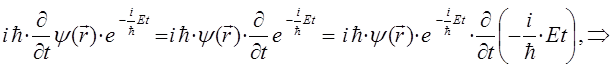
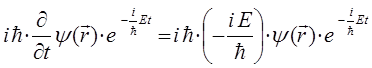
поскольку:
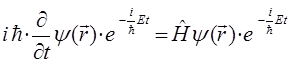
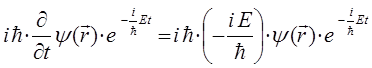
тогда соответственно будем иметь:
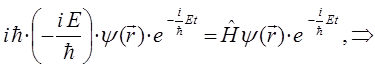

учитывая, что:
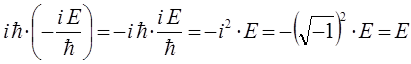
находим, что:
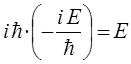
и, следовательно:
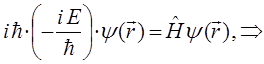
Дата добавления: 2015-03-14; просмотров: 1068;
