Вращательно-колебательные спектры.

Одновременно со сменой колебательного состояния молекулы изменяется и его вращательное состояние. Изменение колебательных и вращательных состояний приводит к возникновению вращательно-колебательных спектров. Колебательная энергия молекул приблизительно в сто раз больше её вращательной энергии, поэтому вращение не нарушает колебательную структуру молекулярных спектров. Наложение небольших в энергетическом отношении вращательных квантов на сравнительно большие по энергии колебательные кванты, смещает линии колебательного спектра в ближнюю инфракрасную область электромагнитного спектра и превращает их в полосы. По этой причине вращательно-колебательный спектр, который наблюдается в близкой инфракрасной области, имеет линейчато-полосатую структуру.

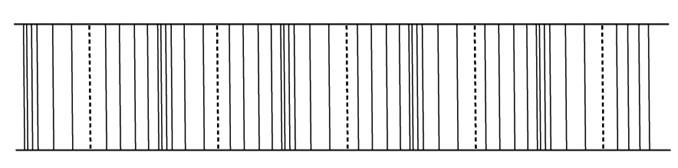
Каждая полоса такого спектра имеет центральную линию (пунктирная линия), частота которой определяется разницей колебательных термов молекулы. Совокупность таких частот представляет чистый колебательный спектр молекулы. Квантово-механические расчёты, связанные с решением волнового уравнения Шрёдингера с учётом взаимного влияния вращательных и колебательных состояний молекулы, приводят к выражению:

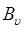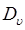где и не являются постоянными для всех энергетических уровней и зависят от колебательного квантового числа.

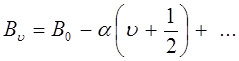
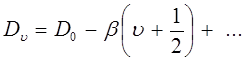
где 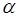и 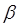- постоянные, меньшие по величине, чем 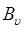и 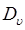. В силу малости параметров 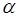и 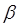, в сравнении с величинам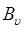и и 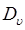, вторыми слагаемыми в данных соотношениях можно пренебречь и рассматривать собственно вращательно-колебательную энергию молекулы, как сумму колебательной и вращательной энергии жёсткой молекулы 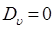, тогда соответственно выражение:

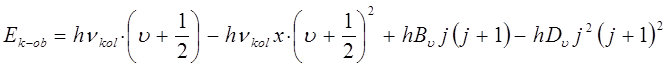
может быть преобразовано далее к виду:

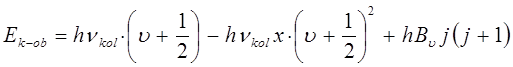
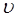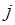Это выражение хорошо передаёт структуру спектра и приводит к искажению только при больших значениях квантовых чисел и . Рассмотрим вращательную структуру вращательно-колебательного спектра. Так, при излучении, молекула переходит с высших энергетических уровне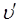й и 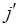на нижние, и в спектре появляются линии с частотами:

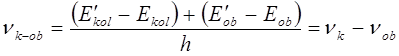
т.е. для частоты линии вращательно-колебательного спектра можно записать соответственно:

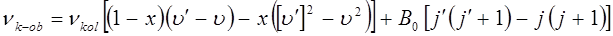
совокупность частот даёт вращательно-колебательный спектр. Первый член в данном уравнении выражает спектральную частоту, возникающую при изменении только лишь колебательной энергии 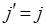. Рассмотрим распределение вращательных линий в полосах спектра. В границах одной полосы её тонкая вращательная структура определяется только лишь значением вращательного квантового числа 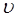. Для такой полосы можно записать в виде:

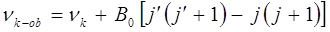
где

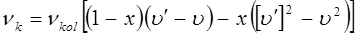
Согласно правилу отбора Паули:

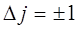
вся полоса разделяется на две группы спектральных серий, которые располагаются относительно 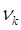по обе стороны. Действительно, если:

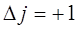
т.е. когда:

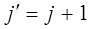
то получаем группу линий:

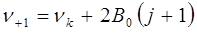
если же:

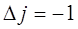
т.е. когда:

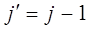
то получаем группу линий:

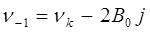
В случае переходов 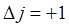когда молекула переходит с 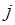- го вращательного уровня на 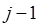вращательный энергетический уровень, возникает группа спектральных линий с частотами 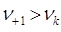. Эта группа линий называется позитивной или 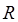- веткой полосы спектра, начинающаяся с 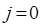. При переходах 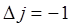, когда молекула переходит с 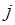-го на 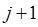энергетический уровень, возникает группа спектральных линий, с частотами 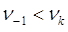. Эта группа линий называется негативной или 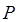- веткой полосы спектра, начинающаяся с 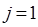. Это объясняется тем, что значение 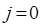, что отвечает 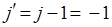не имеющего физического смысла. - и - ветки полосы, на основании уравнений вида:

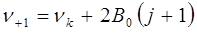
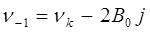
состоят из линий:

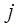
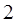
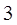
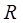
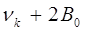
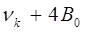
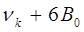
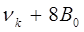
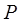
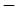
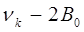
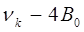
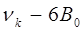
Таким образом, каждая полоса вращательно-колебательного спектра состоит из двух групп равноудалённых линий с расстоянием между соседними линиями:

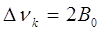
для реальной нежёсткой молекулы, учитывая уравнение:

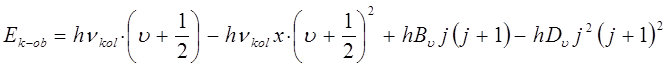
для частоты лини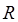й - и 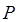- веток полосы, получаем:

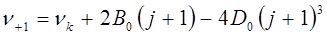
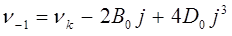
Вследствие этого лини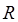и - и 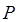- веток искривляются и наблюдаются не равноудалённые линии, а 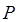- ветки, которые расходятся и 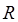- ветки, которые сближаются с образованием канта полосы. Таким образом, квантовая теория молекулярных спектров оказалась способной при расшифровке спектральных полос в ближней инфракрасной области, трактуя их как результат одновременного изменения вращательной и колебательной энергии. Необходимо отметить, что молекулярные спектры являются ценным источником сведений о строении молекул. Изучая молекулярные спектры, можно непосредственно определить различные дискретные энергетические состояния молекул и на основании полученных данных сделать надёжные и точные выводы относительно движения электронов, колебания и вращения ядер в молекуле, а также получить точные сведения относительно сил действующих между атомами в молекулах, межъядерных расстояниях и геометрическом расположении ядер в молекулах, энергии диссоциации самой молекулы и др.