Колебательные спектры. 4 страница

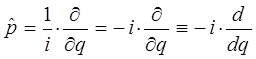
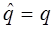
Состояние	Энергия

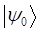
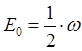
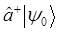
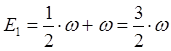
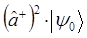
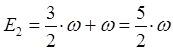
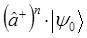
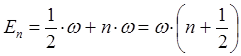
тогда соответственно будем иметь:

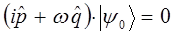
учитывая, что:

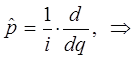
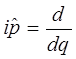
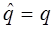
поэтому:

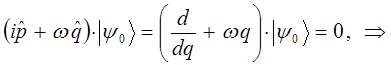
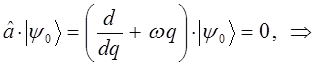
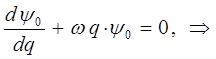
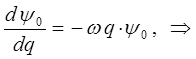
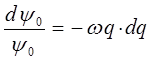
Интегрируя правую и левую части полученного дифференциального уравнения, приходим к выражению:

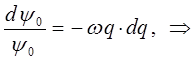
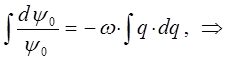
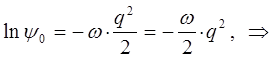
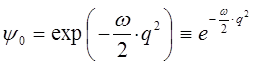
учитывая, что:

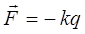
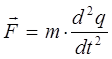
имеем для случая классического (гармонического) осциллятора:

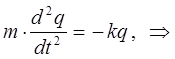
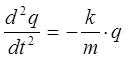
полагая:

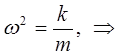
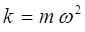
имеем:

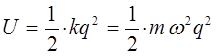
Учитывая приведенные выше соображения, не трудно записать выражение для Гамильтониана в операторной и координатной формах. Операторная форма:

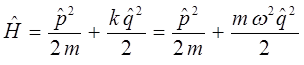
координатная форма:

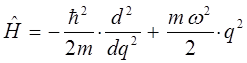
поскольку:

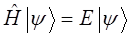
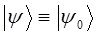
тогда:

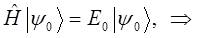
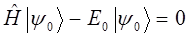
подставляя функцию вида:

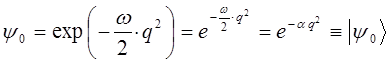
в уравнение:

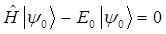
где как было показано выше:

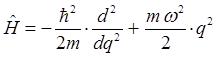
будем иметь соответственно:

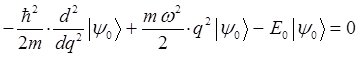
с учётом выражения:

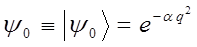
имеем:

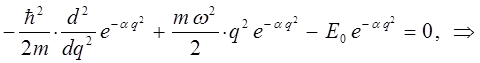
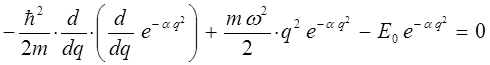
Для упрощения дальнейших выкладок, вычислим отдельно выражение:

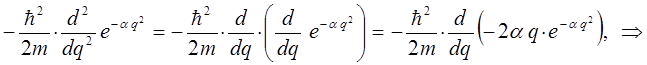
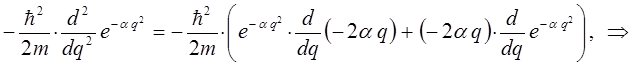
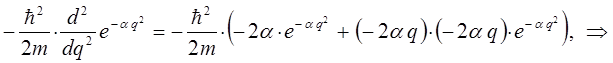
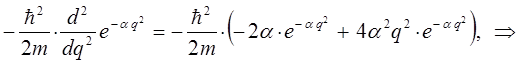
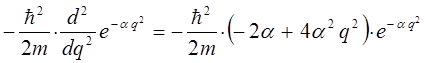
Полученное выражение подставим теперь в соответствующее операторное уравнение вида:

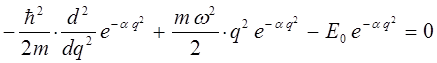
имеем:

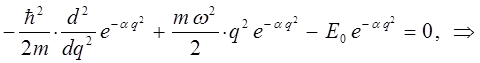
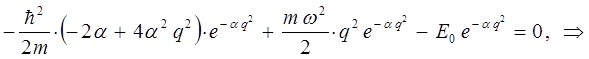
поскольку:

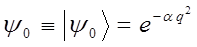
имеем:

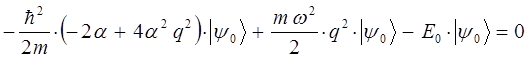
Сокращая полученное выражение на общий член 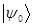, получим тождество вида:

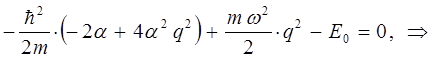
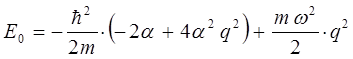
Преобразовывая полученное выражение далее, будем иметь соответственно:

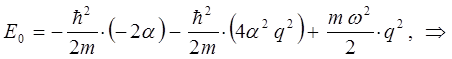
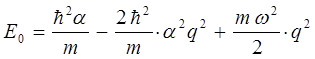
Поскольку коэффициенты при одинаковых степенях обращаются в нуль:

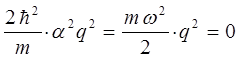
и выражение определяющее энергию нулевых колебаний квантового осциллятора 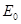будет иметь вид:

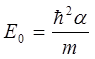
для нахождения коэффициента 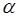, входящего в выражение для энергии нулевых колебаний 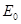, воспользуемся вторым и третьим членами исходного уравнения для энергии нулевых колебаний квантового осциллятора:

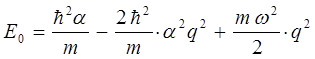
имеем:

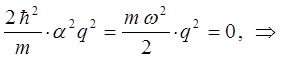
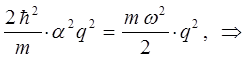
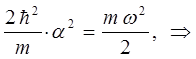
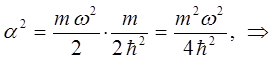
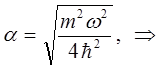
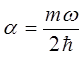
тогда после подстановки полученного выражения в найденное выше уравнение для энергии нулевых колебаний, будем иметь соответственно:

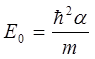
откуда следует, что:

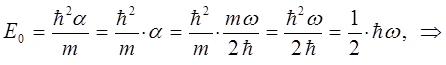
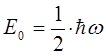
с учётом приведенных выше выкладок, записанное ранее выражение для энергии нулевых колебаний :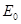

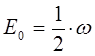
может быть уточнено и записано в виде:

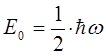
и аналогично:

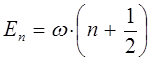
может быть далее представлено к виду:

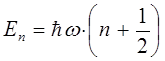
учитывая, что:

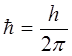
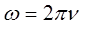
будем иметь соответственно:

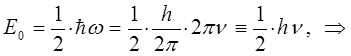
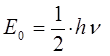
и аналогично получаем:

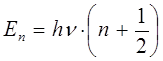
В полученном выше уравнении n представляет целое положительное число, включая нулевое его значение. В теории колебательных спектров его обычно заменяют более адаптированным v - колебательным квантовым числом, тогда соответственно будем иметь:

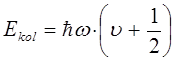
или

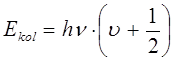
К подобному выражению для колебательной энергии молекулы можно прийти и другим путём. Спектр квантового осциллятора, описываемый уравнениями вида:

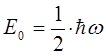
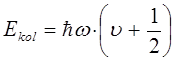
или

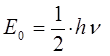
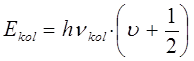
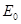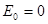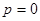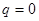называется эквидистантным или равноотстоящим. Необходимо отметить, что наименьшая энергия начинается с ненулевого значения, тогда как в классической механике (состояние покоя и ). Таким образом квантовый осциллятор, в отличие от своего классического аналога, никогда не находится в состоянии покоя. Даже в состоянии с наименьшей энергией 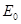частица колеблется (что находится в полном соответствии с принципом неопределённости Гейзенберга):

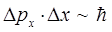
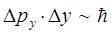
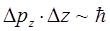
если бы такого не происходило (отсутствовала энергия нулевых колебаний 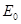), тогда в силу вступали бы законы классической механики, т.е. существовала бы возможность одновременного измерения двух физических величин – координаты и импульса частицы. Существование ненулевого значения энергии 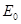находит своё отражение в физических явлениях, возникающих при низких температурах (в том числе и при 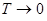). Так, рассеяние света кристаллами обусловлено колебаниями атомов кристаллической решётки. При понижении температуры, амплитуда колебаний понижается, однако сами колебания как показали экспериментальные данные, не прекращаются и вблизи абсолютного нуля. Это в свою очередь приводит к соответствующему рассеянию света.

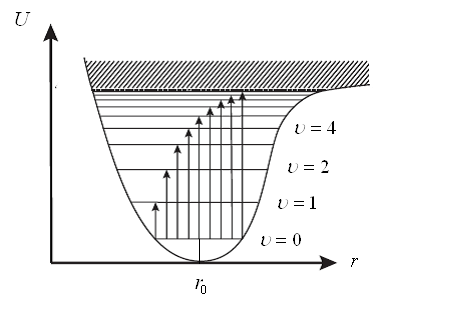
Рис. 4. Ангармонизм колебаний осциллятора.

Другой важный пример – нулевые колебания вакуума. Так, электромагнитное поле описывается набором осцилляторов, представляющих колебания векторов напряжённости электрического 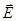и магнитного 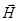поля. Квантование осцилляторов поля позволяет правильно интерпретировать основное его состояние – вакуум. Так, в вакууме 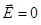, но из-за нулевых колебаний электромагнитное поле флуктуирует, т.е. 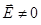. Это, в свою очередь, приводит к флуктуациям координаты электрона в атомах и молекулах, а, следовательно, к смещению всех энергетических уровней (так называемый лэмбовский сдвиг). Хотя сам сдвиг и незначителен (например, в атоме кислорода 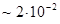эВ), он имеет принципиальное значение, подтверждая таким образом, существование наличия нулевых колебаний и таким образом основные концепции квантовой механики. Ещё одной особенностью энергетических уровней квантового осциллятора является их эквидистантность. Это означает, что расстояние между двумя соседними уровнями является постоянной для данного осциллятора величиной. Для доказательства справедливости данного утверждения, найдём разность энергий двух соседних энергетических уровней:

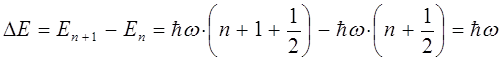
Следовательно, разность энергий между двумя соседними энергетическими уровнями 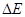не зависит от колебательного квантового числа 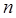, энергетические уровни находятся на одинаковом расстоянии друг от друга. При этом переход осциллятора из возбуждённого состояния 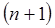в основное 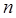, сопровождается излучением кванта энергии 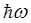. В реальной молекуле потенциальная энергия резко увеличивается только при сближении атомов. При увеличении же межъядерного расстояния сила химической связи постепенно снижается до нуля, а потенциальная энергия возрастает до некоторого постоянного значения, отвечающего потенциальной энергии свободных атомов. Малые колебания двухатомной молекулы можно рассматривать как колебания гармонического осциллятора. При значительных колебаниях молекулы они становятся ангармоническими. По этой причине необходимо подобрать такое выражение функции φ(ρ), которое бы хорошо передавало ангармонизм колебаний молекулы.

Хорошее приближение даёт формула предложенная Морзе (функция Морзе):

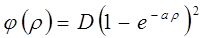
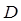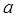где и - некоторые постоянные для данной молекулы величины.

Таким образом, ангармонические колебания двухатомной молекулы можно описать уравнением вида:

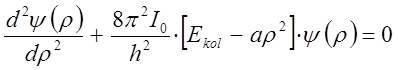
или с учётом функции Морзе:

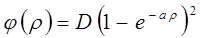
имеем соответственно:

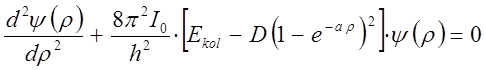
или что то же самое:

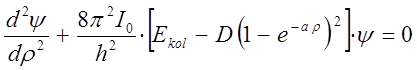
Решение такого уравнения даёт выражение для колебательной энергии двухатомной молекулы:

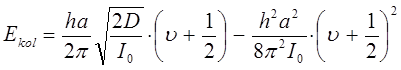
вводя обозначения:

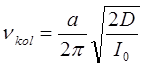
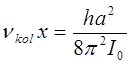
получаем уравнение:

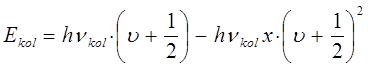
тождественное найденному уже ранее эмпирическому уравнению вида:

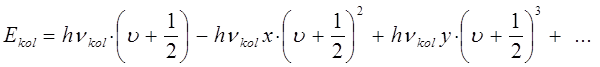
Таким образом, ближнюю инфракрасную область электромагнитного спектра можно интерпретировать как колебательный спектр молекул. Квантовая теория колебательных спектров пришла к следующим выводам относительно колебательной энергии молекул. Во-первых, колебательная энергия является величиной, кратной полуцелым числам квантов. Во-вторых, уравнение:

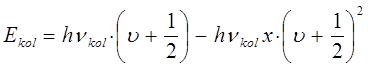
показывает, что на нижнем энергетическом уровне, т.е. при 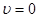колебательная энергия молекулы не равна нулю, что в объясняется наличием у осциллятора так называемых нулевых колебаний. Выражение вида:

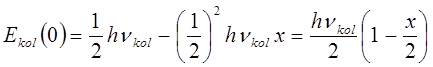
называется нулевой колебательной энергией. Оно показывает величину колебательной энергии молекулы в нормальном колебательном состоянии, а это означает, что и при абсолютном нуле в молекуле имеют место колебательные движения. Квантовая теория показывает, что поглощение и излучение света гармоническим осциллятором может происходить лишь при переходе между соседними уровнями, квантовые числа которых отличаются на единицу. В случае гармонического осциллятора квантовые переходы подчиняются правилу отбора:

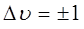
по этой причине в спектре имеется одна линия с частотой, соответствующей собственной частоте гармонического осциллятора:

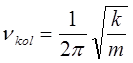
На основании выражения вида:

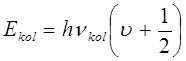
имеем соответственно:

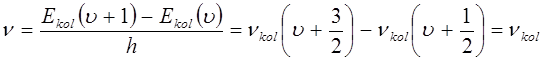
Как это видно из приведенных выкладок, колебательные энергетические уровни гармонического осциллятора будут располагаться на одинаковых расстояниях друг от друга 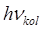. Для реальной молекулы – ангармонического осциллятора – колебательные энергетические уровни сгущаются (уплотняются) при увеличении энергии – значений колебательного квантового числа 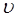. Найдём расстояния между соседними энергетическими уровнями осциллятора:

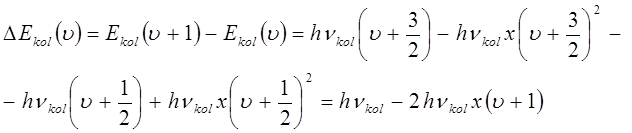
Как это видно их полученного выше выражения, разница между соседними энергетическими уровнями уменьшается на величину 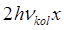с увеличением колебательного квантового числа 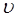, т.е. колебательный спектр реальной молекулы состоит не из одной линии, как это имело место для классического случая, а из серии линий. Поглощение и излучение света с изменением колебательного квантового числа становится возможным при любых переходах. Это в свою очередь означает, что вместе с основной частотой молекула может поглощать или излучать так называемые обертоны. Так, на основании полученного нами ранее выражения:

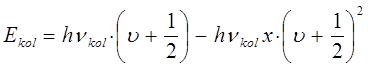
и правила отбора для 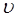, колебательный спектр молекулы будет состоять из линий, имеющих частоту:

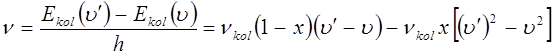
Данное выражение показывает, что колебательный спектр двухатомной молекулы можно представить как совокупность определённых серий спектральных линий. Линии каждой спектральной серии колебательного спектра сближаются, стремясь к некоторой границе, располагающейся в области более коротких длин волн. Границу схождения линий в колебательном спектре будет определять такое максимальное значение колебательного квантового числа 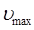, при котором дальнейшее его увеличение не будет приводить к увеличению колебательной энергии. Это в свою очередь задаётся условием вида:

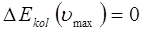
На основании уравнения вида:

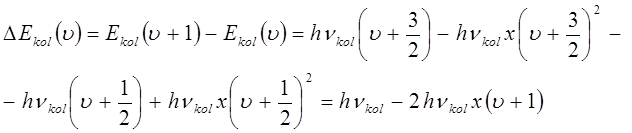
находим, что:

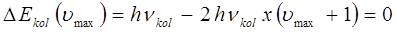
откуда следует, что:

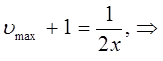
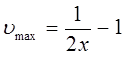
Подставив значение 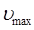в уравнение:

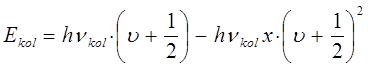
не трудно получить выражение для максимальной колебательной энергии молекулы, т.е. собственно выражение для границы схождения колебательных уровней. Таким образом, имеем соответственно:

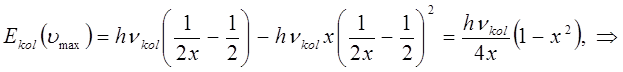
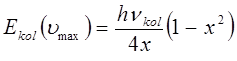
Выражение перед скобками есть энергия диссоциации молекулы. Действительно, совместное решение уравнений относительно :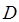

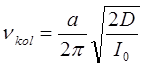
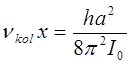
приводит к выражению вида:

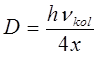
и таким образом

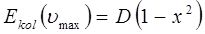
поскольку 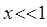, тогда соответственно вторым множителем в полученном выше уравнении можно пренебречь и свести его к выражению вида:

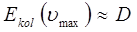
Таким образом, мы приходим к выводу о том, что колебательная энергия двухатомной молекулы не может превышать её энергию диссоциации.

Границей схождения колебательных уровней энергии молекулы служит асимптота, к которой и стремится потенциальная энергия при увеличении расстояния между атомами в молекуле. Это означает, в свою очередь, что для нахождения энергии диссоциации, энергии химической связи в молекуле на основании данных по её колебательным спектрам, достаточно найти некоторую частоту границы схождения спектральных линий при увеличении колебательного квантового числа 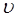. Колебательные спектры многоатомных молекул обычно интерпретируются на основе учения о симметрии молекул и теории групп. Математический аппарат теории групп позволяет вычислить число частот и правила отбора для молекул различной симметрии. Такая информация, чрезвычайно ценная для определения молекулярных констант, изучения строения молекул и т.д., находит сравнительно малое применение для решения химико-аналитических задач. Для решения этих задач используются так называемые характеристические частоты. Анализ ИК-спектров показал, что некоторые из наблюдаемых частот можно привести в соответствие с колебаниями отдельных атомов или групп атомов. Характеристические частоты нашли широкое применение в практической спектроскопии для определения строения молекул и проведение качественного анализа по ИК-спектрам.