Колебательные спектры. 3 страница
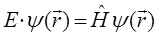
Таким образом, в ходе проделанных выкладок мы показали, что стационарное (не зависящее от времени) уравнение Шрёдингера представляет собой частный случай более общего – нестационарного (допускающего явную зависимость гамильтониана от времени) уравнения:
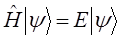
Полученное выражение представляет собой стационарное уравнение Шрёдингера в операторной форме. Это есть частный случай более общей задачи на собственные значения оператора, имеющей в квантовой механике принципиальное значение:
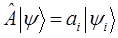
Итак, в ходе проделанных выкладок мы пришли к уравнению вида:
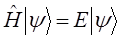
учитывая, что:
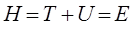
имеем соответственно:
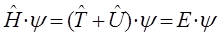
поскольку:
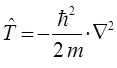
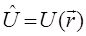
тогда соответственно:
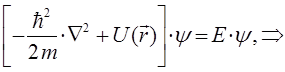
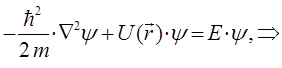
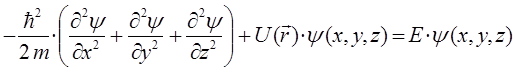
Опуская индексы, делающие полученное уравнение более громоздким, можно записать, что:
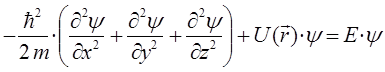
или в более компактном виде:
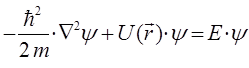
Исходя из теории линейных операторов квантовой механики можно предложить также и другой - операторный путь вывода уравнения Шрёдингера, основанный на свойствах самих операторов квантовой механики. Так, на основании соответствия между квантово-механическими операторами и динамическими переменными:
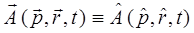
классическое выражение для гамильтониана, имеющее вид:
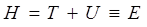
может быть представлено к виду:
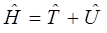
учитывая, что:
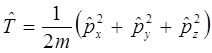
Так, классическое выражение для импульса по-определению имеет вид:
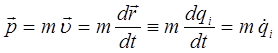
учитывая, что:
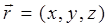
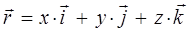
будем иметь соответственно:
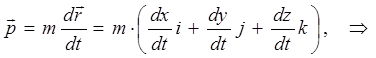
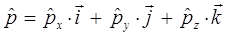
Поскольку любой динамической переменной в квантовой механике ставится в соответствие линейный самосопряжённый оператор:
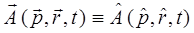
тогда соответственно выражение для импульса, выраженное через его проекции на три не эквивалентных направления в пространстве преобразуется к виду:
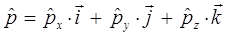
Значение оператора импульса и его компонент можно получить путём решения задачи на собственные значения оператора:
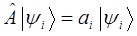
Для этого воспользуемся аналитическим выражением плоской волны де Бройля, полученным уже нами ранее:
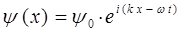
учитывая также, что:
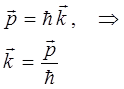
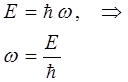
тогда:
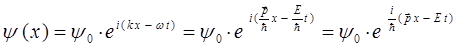
имеем таким образом:
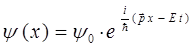
Воспользовавшись уравнением плоской волны де Бройля, решим теперь задачу на собственные значения оператора импульса (его компоненты):
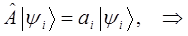
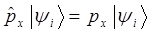
поскольку:
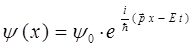
и функция 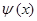 находится по обе стороны операторного уравнения:
находится по обе стороны операторного уравнения:
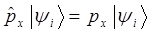
тогда величины амплитуды 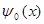 волны сократятся, поэтому:
волны сократятся, поэтому:
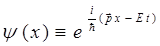
таким образом, имеем:
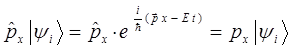
поскольку оператор компоненты импульса 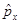 (аналогично
(аналогично 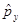 и
и 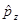 ) – есть дифференциальный оператор, то его действие на волновую функцию (вектор), очевидно, будет сводиться к вычислению частной производной от функции вида:
) – есть дифференциальный оператор, то его действие на волновую функцию (вектор), очевидно, будет сводиться к вычислению частной производной от функции вида:
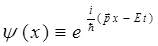
Решая задачу на собственные значения оператора, приходим в выражению:
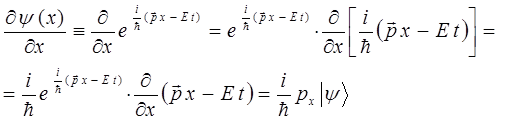
Таким образом, в ходе проделанных выше выкладок, мы пришли к выражению вида:
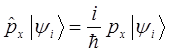
т.к.
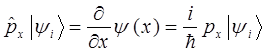
тогда соответственно:
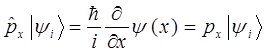
учитывая, что:
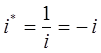
после подстановки получим выражение вида:
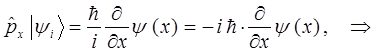
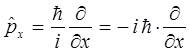
Аналогичным образом можно получить выражения и для других компонент оператора импульса 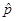 , т.е. имеем:
, т.е. имеем:
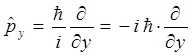
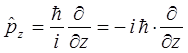
и таким образом выражение для оператора кинетический энергии:
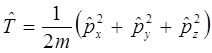
где:
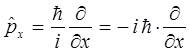
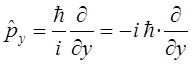
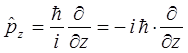
может быть преобразовано далее к виду:
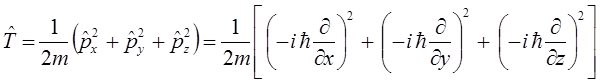
и соответственно:
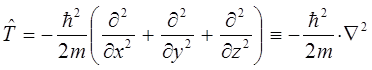
или для оператора полной энергии системы:
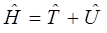
будем иметь соответственно:
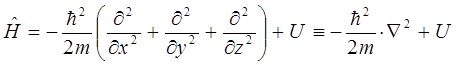
Однако само по себе данное выражение лишено смысла, поскольку операторы представляют собой определённые математические действия, преобразующие исходные функции (вектора) – оригиналы в их линейные отображения. По этой причине будет логично, если оператор полной энергии системы (оператор Гамильтона) будет действовать на некоторую функцию, содержащую в себе всю возможную информацию о свойствах системы частиц, определяющую таким образом всё, что только может быть известно о квантово-механической системе. Такую функцию в квантовой механике называют волновой функцией. Она полностью описывает состояние частицы (системы частиц) в любой момент времени. Учитывая выше сказанное, а также операторное уравнение вида:
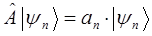
имеем:
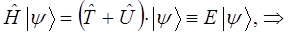
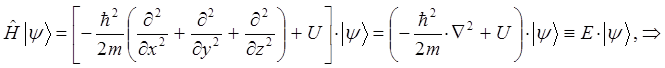
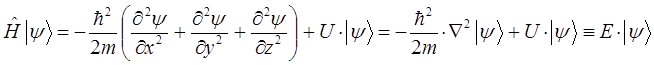
представляя его далее к виду:
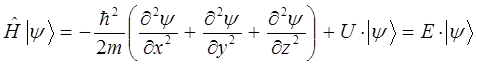
получим:
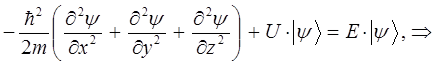
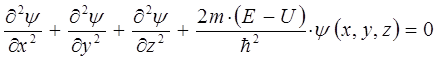
Операторы физических величин (динамических переменных) – координаты, импульса, углового момента, энергии являются линейными самосопряжёнными (эрмитовыми) операторами, следовательно, на основании соответствующей теоремы, их собственные значения являются действительными (вещественными) числами. Именно это обстоятельство и послужило основанием для использования операторов в квантовой механике, поскольку в результате физического эксперимента мы получаем именно действительные величины. В этом случае собственные функции оператора, соответствующие различным собственным значениям, ортогональны. Если мы имеем два различных оператора, то их собственные функции будут различными. Однако если операторы коммутируют между собой, то собственные функции одного оператора будут являться также собственными функциями другого оператора, т.е. системы собственных функций коммутирующих между собой операторов будут совпадать.
Квантово-механические представления о природе колебательных спектров позволили найти эмпирическое уравнение для колебательной энергии молекулы:
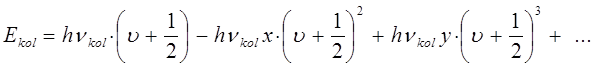
где x, y, … - эмпирически найденные постоянные, называемые также постоянными ангармоничности; v - целое положительно число, которое может принимать все целые значения включая нуль. Как показывает опыт, постоянные ангармоничности квантового осцилятора удовлетворяют следующим требованиям:
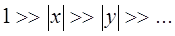
поэтому при небольших значениях v, можно ограничиться первыми двумя членами ряда, т.е. имеем:
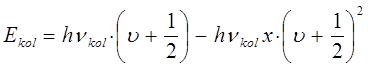
Так, для одномерного случая, полученное нами выше уравнение Шрёдингера очевидно будет иметь вид с учётом приведенной массы молекулы:
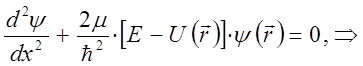
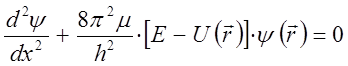
Учитывая понятие относительного отклонения ядер от положения равновесия:
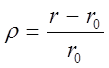
получаем соответственно:
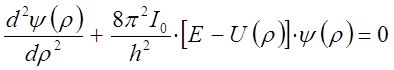
В данном уравнении волновая функция и потенциальная энергия являются функциями переменной ρ. В общем случае для потенциальной энергии является верным выражение:
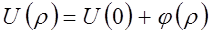
где 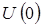 определяется лишь энергетическим состоянием электронов, т.е.
определяется лишь энергетическим состоянием электронов, т.е. 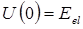 .
.
Функцию φ(ρ) в самом простейшем случае можно представить уравнением параболы:
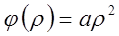
тогда, соответственно, полученное нами выше уравнение вида:
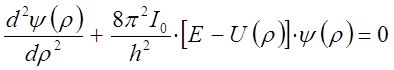
можно решить после соответствующих подстановок в виде:
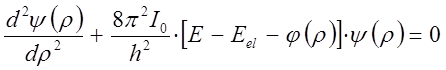
или с учётом параболической зависимости вида:
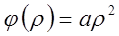
будем иметь соответственно:
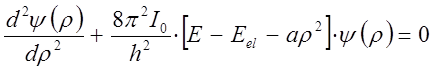
если пренебречь вращательно и ядерной энергией молекулы, т.е. принять:
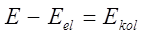
тогда уравнение, описывающее гармонический характер колебаний ядер в молекуле, запишется в виде:
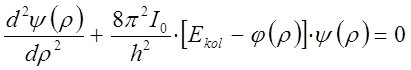
или с учётом выражения:
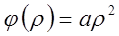
имеем в окончательном виде:
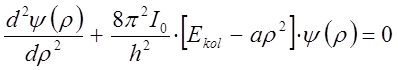
Решение полученного уравнения приводит к выражению для колебательной энергии молекулы:
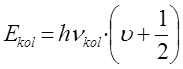
Наиболее просто задача о получении колебательного спектра двухатомной молекулы решается на основании рассмотрении модели так называемого квантового осцилятора. Так, в классической механике с учётом квадратичной зависимости потенциальной энергии от величины смещения  , классический гамильтониан можно представить к виду:
, классический гамильтониан можно представить к виду:
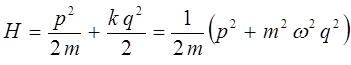
Для упрощения вычислений полагаем, 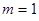 и классический гамильтониан осциллятора тогда берём соответственно в виде:
и классический гамильтониан осциллятора тогда берём соответственно в виде:
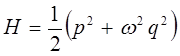
сумму квадратов в полученном выражении удобно представить в виде квадратов модуля комплексной величины:
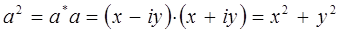
тогда, соответственно будем иметь:
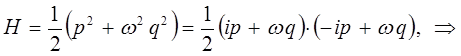
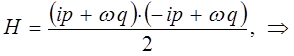
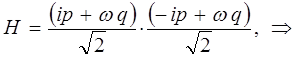
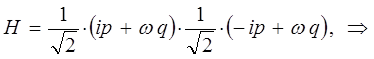
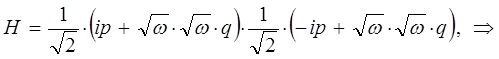
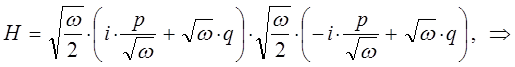
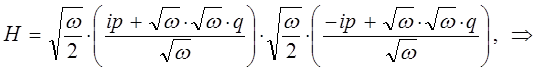
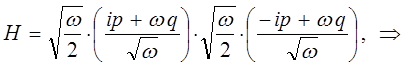
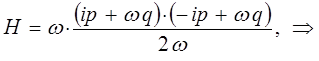
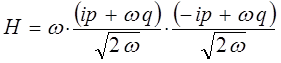
поскольку:
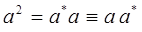
имеем:
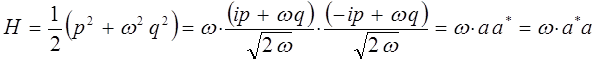
где
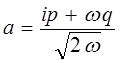
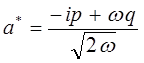
откуда следует, что:
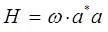
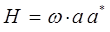
очевидно, что:
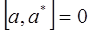
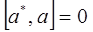
На основании второго постулата квантовой механики имеем:
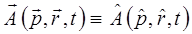
тогда соответственно, выражение:
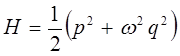
можно будет представить далее к виду:
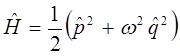
где
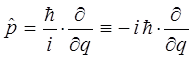
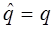
переходя к атомным единицам измерения ( 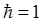 ), перепишем соответствующее выражение для оператора импульса в виде:
), перепишем соответствующее выражение для оператора импульса в виде:
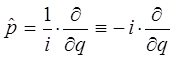
На основании приведенных выше выкладок, строим выражение для оператора Гамильтона, аналогичное:
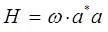
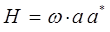
имеем таким образом:
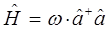
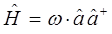
учитывая свойство коммутативности для операторов импульса и координаты:
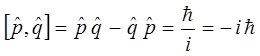
или в атомных единицах измерения по Хартри:
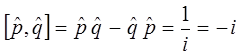
Учитывая приведенные выше выкладки, будем иметь соответственно:
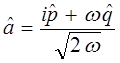
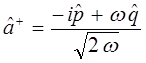
поэтому:
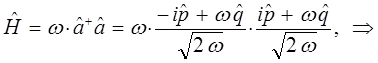
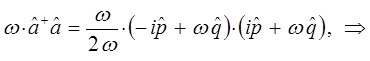
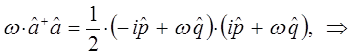
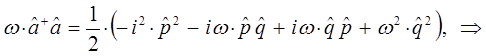
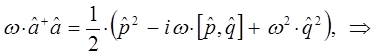
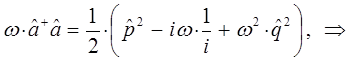
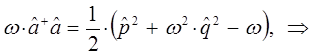
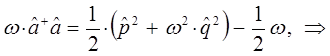
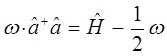
Таким образом, мы пришли к выражению вида:
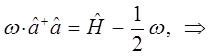
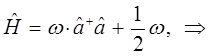
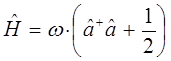
Сравнение выражений для оператора Гамильтона, даёт:
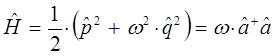
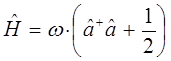
где дополнительный член вида 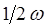 - типично квантовая поправка. Аналогично из второй эквивалентной формы для Гамильтониана вида:
- типично квантовая поправка. Аналогично из второй эквивалентной формы для Гамильтониана вида:
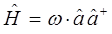
находим соответственно, что:
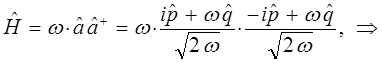
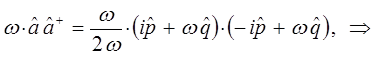
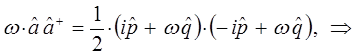
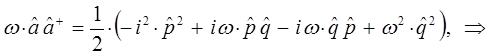
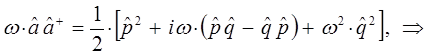
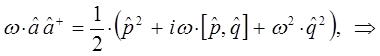
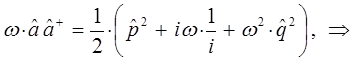
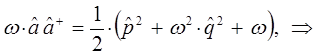
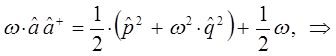
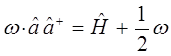
Таким образом, в ходе проделанных выкладок, приходим к выражению вида:
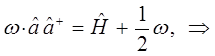
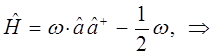
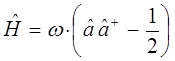
имеем соответственно:
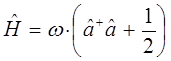
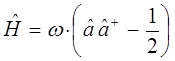
Теперь установим ряд вспомогательных соотношений. Для этих целей, вычислим произведение операторов 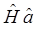 и
и 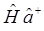 , используя полученные уже ранее выражения вида:
, используя полученные уже ранее выражения вида:
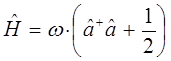
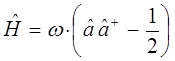
имеем таким образом:
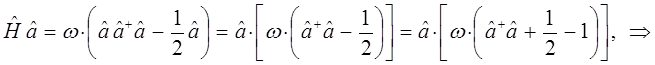
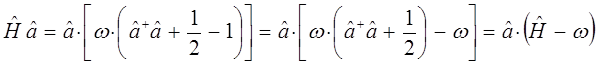
и аналогично:
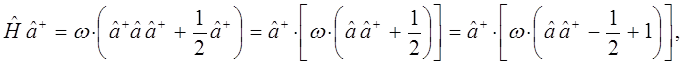
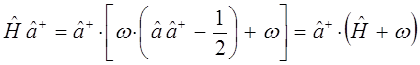
имеем:
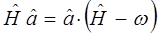
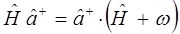
Далее процедура отыскания всех допустимых значений энергии квантового осциллятора состоит в получении эквидистантного спектра. Для этого необходимо решить задачу на собственные значения оператора:
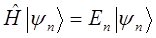
которая легко решается с помощью полученных нами уже выше выражений:
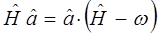
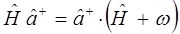
Действительно, пусть 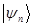 является собственным вектором, удовлетворяющим выражению вида:
является собственным вектором, удовлетворяющим выражению вида:
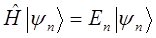
тогда вектора 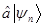 и
и 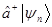 также будут являться собственными векторами этой задачи и произведение операторов
также будут являться собственными векторами этой задачи и произведение операторов 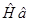 и
и 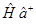 при действии на вектор
при действии на вектор 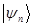 , также будут давать собственные вектора.
, также будут давать собственные вектора.
После соответствующих подстановок, имеем:
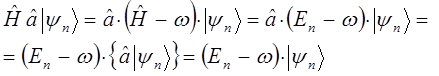
и аналогично:
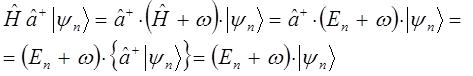
имеем соответственно:
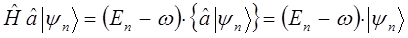
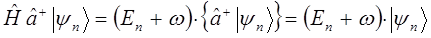
Следовательно, действие оператора 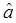 на вектор
на вектор 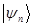 приводит к состоянию с энергией на
приводит к состоянию с энергией на 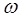 меньше, а действие оператора
меньше, а действие оператора 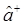 на вектор
на вектор 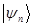 - к состоянию с энергией, на
- к состоянию с энергией, на 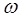 больше (в атомных единицах Хартри, где
больше (в атомных единицах Хартри, где 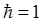 ), т.е. зная
), т.е. зная 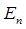 , мы знаем и все остальные энергии. На основании приведенных выше выкладок, построим цепочку собственных векторов и соответствующих им энергий. Эта цепочка не может быть бесконечной, поскольку
, мы знаем и все остальные энергии. На основании приведенных выше выкладок, построим цепочку собственных векторов и соответствующих им энергий. Эта цепочка не может быть бесконечной, поскольку 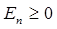 , т.е. все допустимые энергии должны быть положительными величинами. Поэтому в данной цепочке, очевидно, должно существовать некоторое предельное состояние
, т.е. все допустимые энергии должны быть положительными величинами. Поэтому в данной цепочке, очевидно, должно существовать некоторое предельное состояние 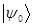 , причём такое, что на нём цепочка будет обрываться:
, причём такое, что на нём цепочка будет обрываться:
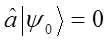
Соответствующая данному состоянию 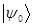 энергия
энергия 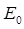 - наименьшая из возможных, т.е. отвечает основному состоянию осциллятора, характеризуя энергию так называемых нулевых колебаний:
- наименьшая из возможных, т.е. отвечает основному состоянию осциллятора, характеризуя энергию так называемых нулевых колебаний:
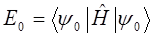
поскольку:
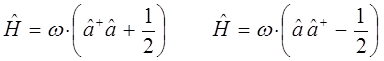
тогда соответственно:
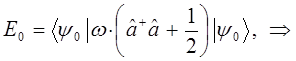
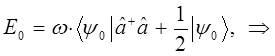
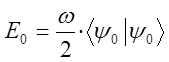
| Состояние | Энергия |
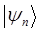
| 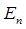
|
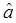
| 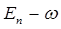
|
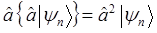
| 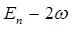
|
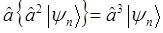
| 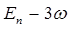
|

| 
|
учитывая, что:
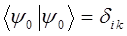
где
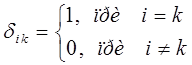
имеем окончательно:
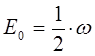
очевидно, как это видно из приведенных выкладок, все выше лежащие состояния квантового осциллятора будут являться возбуждёнными, т.е. будет соблюдаться неравенство вида:
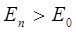
Возбуждённые состояния получают из 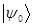 с помощью выражений вида:
с помощью выражений вида:
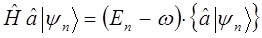
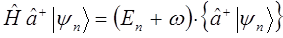
Этот процесс перехода от n -го состояния к 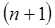 - му, уже ничем не ограничен, здесь
- му, уже ничем не ограничен, здесь 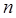 принимает любое целое значение
принимает любое целое значение 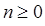 . Явный вид волновых функций легко устанавливается, если известно состояние
. Явный вид волновых функций легко устанавливается, если известно состояние 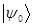 , соответствующее энергии нулевых колебаний.
, соответствующее энергии нулевых колебаний.
Такое состояние находится из уравнения вида:
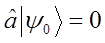
поскольку:
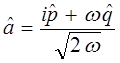
тогда соответственно операторное уравнение:
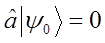
преобразуется к виду:
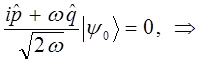
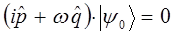
учитывая, что:
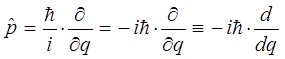
или в атомных единицах Хартри, где 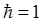 :
:
Дата добавления: 2015-03-14; просмотров: 970;
