Колебательные спектры. 1 страница

Полосы, связанные с возбуждением колебательных уровней энергии, располагаются в области спектра примерно от 200-300 до 400-5000 см^-1, что соответствует энергии квантов от 3 до 60 кДж/моль. Поэтому при обычных температурах энергетическое состояние молекул, как правило, характеризуется основным колебательным уровнем. Простейшей моделью, которая используется при рассмотрении колебаний двухатомной молекулы, является модель гармонического осциллятора. В ней колебательное движение ядер вдоль линии химической связи, приводит к периодическому увеличению и уменьшению межъядерного расстояния, поэтому при малых амплитудах колебаний, молекулу можно представить как гармонический осциллятор - простейший тип колебательного движения. Движение частицы в такой модели представляют собой свободные (собственные) незатухающие механические колебания, т.е. такие колебания, которые совершаются без внешнего воздействия за счёт первоначально полученной телом энергии. Кривая потенциальной энергии в такой модели обычно аппроксимируется параболой. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления. Здесь колеблющаяся величина (материальная точка) с массой 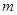изменяется со временем по закону синуса или косинуса. Вдоль одной из координатных осей на неё действует упругая возвращающая сила 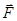. Очевидно, при малых отклонениях частицы (материальной точки) от положения равновесия, под действием упругой возвращающей силы 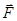, будут совершаться колебания относительно этой точки равновесия. Примерами гармонического осциллятора являются пружинный (материальная точка на пружине), математический и физический маятники, а также колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными). Для рассматриваемой системы гармонического осциллятора, очевидно, будут справедливы условия вида:

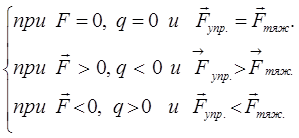
Пусть у нас имеется некоторое тело массой – m (материальная точка), подвешенное на пружине жёсткостью 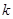. В этом положении упругая сила 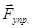, приложенная к телу, уравновешивает силу тяжести 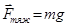, т.е. в данном случае справедливо равенство вида:

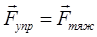
Смещение материальной точки относительно оси 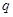(положение равновесия) равно нулю, т.е. 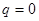. Если к телу приложить некоторую силу 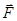, оттянув пружину (сместив данное тело из положения равновесия, при котором 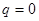), то тело выйдет из состояния равновесия. При этом на тело будет действовать большая упругая сила 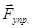, которая будет тем больше, чем больше смещение 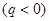будет получать подвешенное на пружине тело. Согласно закону Гука, при упругих деформациях возникает сила, направленная к положению равновесия и пропорциональная смещению тела (деформации). Силы, неупругие по природе, но аналогичные по-свойствам, называют квазиупругими. Квазиупругие силы возникают при малых деформациях. Таким образом, изменение упругой силы, пропорционально изменению длины пружины или смещению тела:

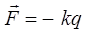
здесь k – коэффициент пропорциональности (жёсткость пружины). Здесь знак минус показывает, что возвращающая сила 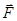всегда направлена в сторону положения равновесия.

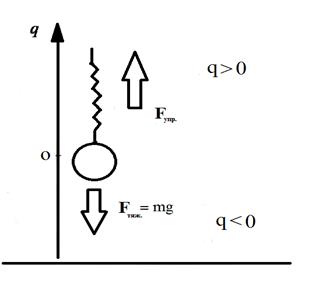
Рис. 3. Модель гармонического осциллятора

На основании второго закона Ньютона:

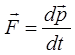
а также учитывая, что:

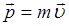
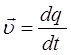
получим дифференциальное уравнение, описывающее движение материальной точки:

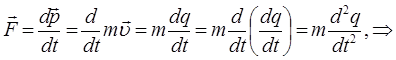
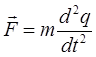
преобразуем полученное выражение к виду:

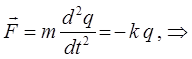
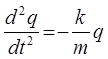
примем:

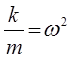
откуда:

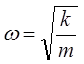
тогда:

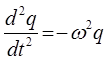
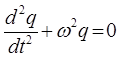
полученное выражение представляет собой линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

В общем случае, линейным дифференциальным уравнением второго порядка называется уравнение первой степени, линейное относительно неизвестной функции и её производных. Будем записывать такое уравнение в виде:

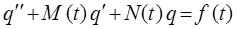
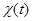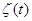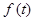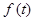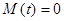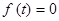здесь и – постоянные. Функция называется правой частью уравнения. Если функция тождественно равна нулю (как в нашем случае), то такое уравнение называется линейным уравнением без правой части (или однородным). В противном случае – линейным уравнением с правой частью (или неоднородным). Достаточно очевидно, что при и , дифференциальное уравнение:

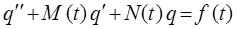
сводится к уравнению вида:

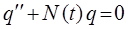
в данном уравнении:

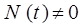
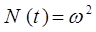
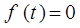
Теорема 1: «Если q₁(t) и q₂(t) – решения линейного уравнения 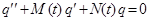, то функция вида 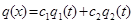при любых постоянных c₁ и c₂ , также является решением уравнения. Здесь выражение 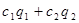является линейной комбинацией соответствующих частных решений q₁ и q_2.». Из сказанного выше можно заключить, что если q₁ и q₂ – решения уравнения:

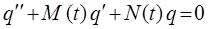
такие, что их отношение не равно постоянной величине:

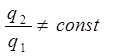
то линейная комбинация этих функций 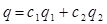, является решением дифференциального уравнения. Нахождение общего решения дифференциального уравнения принципиально, т.к. из общего решения при любых заданных условиях может быть найдено частное решение, удовлетворяющее этим условиям. Для проверки линейной независимости функций q₁ и q₂, являющихся частными решениями дифференциального уравнения, необходимо составить и решить так называемый определитель Вронского (Вронскиан) W. При этом Вронскиан не должен обращаться в нуль, т.е. :

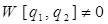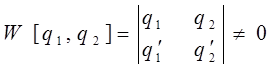
Обычно частные решения дифференциального уравнения ищут в виде показательной функции 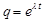, где l - постоянная величина. Такой выбор вида частного решения обусловлен тем, что это единственная элементарная функция, все производные которой подобны между собой и к самой функции. Функцию вида 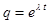называют ещё стандартной подстановкой. Дифференцируя функцию 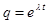, беря вначале первую, а затем вторую производную:

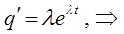
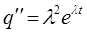
итак, имеем соответственно:

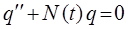
Очевидно подстановка значения 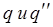в данное уравнение, даст выражение вида:

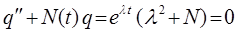
Поскольку 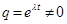, то из последнего уравнения следует, что:

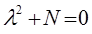
такое уравнение относительно l, называется характеристическим уравнением, отвечающим соответствующему дифференциальному уравнению:

,

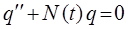а функция 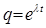является стандартной подстановкой (частным решением дифференциального уравнения), с помощью, которой решается исходное дифференциальное уравнение. При этом, 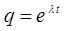будет частным решением соответствующего уравнения лишь в том случае, если l - корень характеристического уравнения. Таким образом, для решения искомого дифференциального уравнения необходимо составить и решить характеристическое уравнение. Чтобы составить характеристическое уравнение, нужно в данном дифференциальном уравнении заменить q единицей, а производную искомой функции 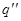– величиной l в степени, равной порядку производной l² соответственно. Следует различать три возможных случая для корней l₁ и l₂ характеристического уравнения (предполагается, что коэффициенты M и N – действительные числа):

· l₁ и l₂ – корни уравнения действительные и различные числа, т.е. .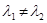

· l₁ и l₂ - корни уравнения действительные и равные числа, т.е. .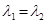

· l₁ и l₂ - корни уравнения комплексные сопряжённые числа: l₁ = a + ib

и l₂ = a - ib ( ).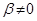

Учитывая, что:

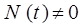
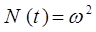
представим уравнение:

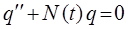
к виду:

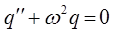
запишем теперь, в соответствии с правилами указанными выше, характеристическое уравнение:

,

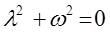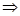
l₁ = iw ,

l₂ = - iw

имеем соответственно два независимых решения искомого дифференциального уравнения. Таким образом, решив характеристическое уравнение, мы приходим к выводу о том, что корни уравнения – комплексно сопряжённые числа (третий из выше перечисленных случаев). В соответствии с приведенной выше теоремой об общем решении дифференциального уравнения, в независимости от того являются ли корни характеристического уравнения действительными или комплексными сопряжёнными числами, общее решение имеет вид:

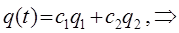
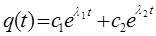
поскольку в нашем случае, корни характеристического уравнения являются комплексными сопряжёнными числами, т.е. имеет место два независимых решения:

l₁ = a + ib,

l₂ = a - ib,

общее решение можно записать в виде:

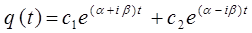
здесь с₁ и с₂ –произвольные комплексные постоянные. Учитывая, что:

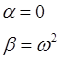
тогда на основании выше приведенных выкладок можно заключить, что:

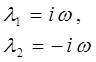
Учитывая, что общее решение дифференциального уравнения строится как суперпозиция частных решений:

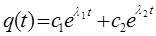
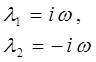
будем иметь соответственно уравнение вида:

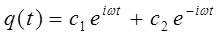
здесь частными являются решения вида:

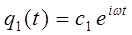и

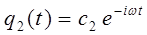
на основании известных из курса линейной алгебры формул Эйлера:

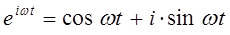
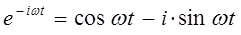
из которых следует, что:

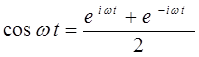
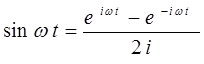
а также принимая, что:

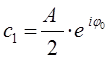
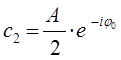
получим соответственно уравнение вида:

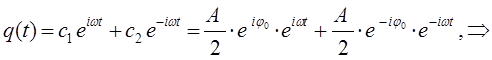
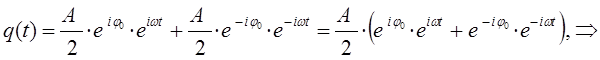
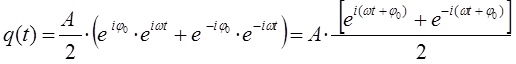
поскольку по-определению:

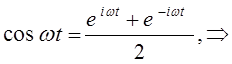
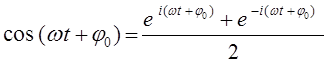
тогда выражение вида:

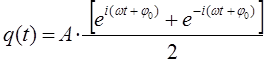
очевидно, может быть представлено к виду:

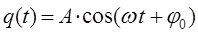
если же принять, что:

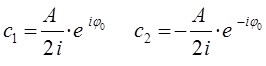
тогда будем иметь соответственно:

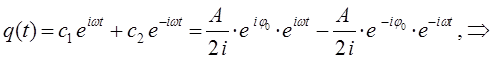
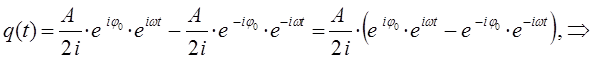
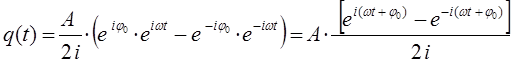
поскольку:

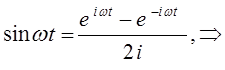
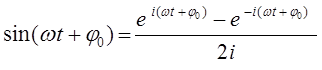
тогда выражение:

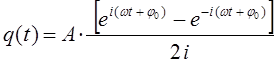
очевидно, может быть далее представлено к виду:

Таким образом, путём соответствующих преобразований, на основании общего решения дифференциального уравнения:

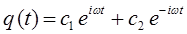
мы пришли к двум эквивалентным друг другу решениям дифференциального уравнения, записанным в тригонометрической формах:

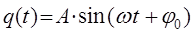
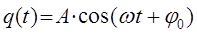
Здесь величина 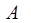есть амплитуда колебания, характеризующая размах колебательного движения, величину смещения материальной точки от положения равновесия. Аргумент 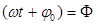называется фазой колебания, а 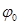- начальной фазой колебания в момент времени 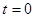. Достаточно очевидно, что:

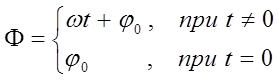
Расстояние, отделяющее колеблющуюся точку от положения равновесия, характеризует величина 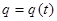. В общем случае амплитуда и начальная фаза колебания определяются начальными условиями движения, т.е. положением и скоростью материальной точки в момент времени 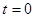. Среди различных видов колебательного движения, гармонические колебания являются наиболее простыми. Необходимо отметить, что поскольку величина 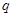характеризует смещение материальной точки от положения равновесия, а величина 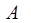- амплитуду колебательного движения (размах колебания), тогда на основании условия вида:

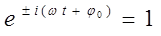
величина смещения 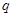будет сводиться к величине, 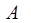и будет характеризовать, таким образом, максимальное отклонение колеблющейся материальной точки от положения равновесия, т.е. будет справедливо уравнение вида:

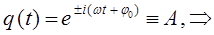и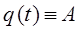

Необходимо также отметить, что при преобразовании дифференциального уравнения, описывающего колебания гармонического осциллятора, величина 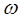была введена чисто формально, в то время как она имеет глубокий физический смысл, определяя частоту колебаний.

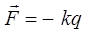
учитывая, что:

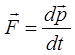
тогда соответственно:

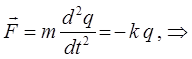
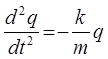
принимая что:

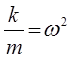
имеем:

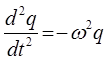
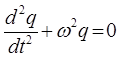
Величина 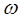называется круговой (циклической) частотой. Выведенное для гармонического осциллятора дифференциальное уравнение, показывает, что данная величина зависит от жёсткости пружины и массы материальной точки.

Аналогичная угловой скорости 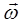, она связывает линейную скорость и период колебаний, представляя, таким образом, число периодов колебаний, за которые фаза колебания получит приращение 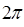. Это становится очевидным из следующих рассуждений. Поскольку формально:

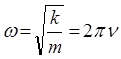
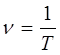
тогда соответственно:

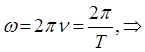
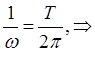
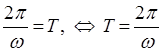
Очевидно, чем больше по величине будет круговая (циклическая) частота, тем меньше будет величина периода колебательного движения. Проводя аналогию между угловой скоростью и циклической частотой, можно увидеть, что чем больше будет скорость, с которой колеблющаяся точка совершит полный оборот на 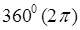при своём движении, получая, таким образом, приращение 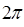, тем за меньшее время будет совершено системой колебательное движение. Необходимо отметить ещё один немаловажный факт, следующий из приведенных выше соображений. Имеем соответственно:

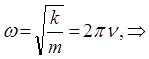
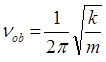
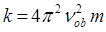
Для вычисления допустимых значений энергии гармонического осциллятора в квантовой механике, необходимо решить задачу на собственные значения оператора полной энергии системы 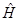. Так, на основании уравнения вида:

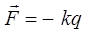
можно найти потенциальную энергию гармонического осциллятора. Известно, что сила, определяется как:

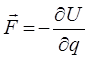
или при рассмотрении одномерного движения частицы массой m вдоль одной из координатных осей, имеем соответственно:

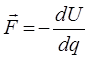
Учитывая уравнения описывающие смещение частицы массой m при движении гармонического осциллятора:

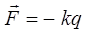
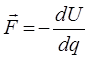
будем иметь соответственно:

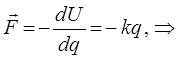
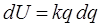
Интегрирование полученного выражения:

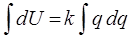
приводит к уравнению вида:

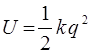
Полученные результаты позволяют сделать следующие выводы. Во-первых, гармонический осциллятор можно определить как систему, потенциальная энергия которой параболически зависит от смещения частицы из состояния равновесия. Во-вторых, гармонический осциллятор имеет одну частоту колебания. В то же самое время, его полная энергия может принимать произвольные значения:

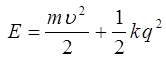
Основываясь на представлениях классической механики, можно говорить только об одной линии в колебательном спектре двухатомной молекулы с частотой ν_ob, отвечающей всем возможным изменениям в колебательных энергетических состояниях. Однако исследования спектров поглощения двухатомных молекул показали, что они содержат несколько линий. Это указывает в свою очередь на то, что колебания ядер реальных молекул значительно отличаются от классического приближения. Это связано, прежде всего, с тем, что при увеличении расстояния между ядрами, энергия взаимодействия между ними при достаточно больших расстояниях снижается до нуля и ведёт к исчезновению связи между ядрами в молекуле - диссоциации частицы на атомы. Таким образом, колебания атомов в реальных молекулах являются ангармоническими. В отличие от классической механики, которая говорит о непрерывном изменении полной энергии осциллятора, квантовая механика напротив, даёт для него набор дискретных уровней колебательной энергии. В основе таких представлений лежат расчёты, основанные на решении волнового уравнения Шрёдингера, которое можно получить на основании оптико-механической аналогии Гамильтона. Так, при выводе уравнения Шрёдингера достаточно удобным является рассмотрение движения частицы в центральном поле сил. Характерными примерами систем такого типа является гармонический осциллятор и движение частицы в кулоновском поле сил. Обычно более общая теория может быть сформулирована логически замкнутым образом не зависимо от менее общей теории, являющейся её предельным случаем. Так, релятивисткая механика может быть построена на основании своих принципов, без всяких ссылок на ньютоновскую механику. Формулировка же основных положений квантовой механики, принципиально невозможна без привлечения механики классической. Таким образом, квантовая механика содержит в себе классическую в качестве своего предельного случая. Мало того, она нуждается в этом самом предельном случае для самого своего обоснования. При этом переход от классической механики к квантовой, осуществляется через механику колебаний и волн по-аналогии с тем, как происходит предельный переход от волновой к геометрической оптике. Необходимо подчеркнуть, что указанный выше предельный переход не только неизбежен, но и необходим. Он позволяет представить квантовую механику не как систему постулатов «загадочного» происхождения, а как стройную физическую теорию с определённым логическим выводом (терминологически и идейно) из классического подхода. Так, при рассмотрении движения частицы в центральном поле сил, путём соответствующих преобразований, на основании общего решения дифференциального уравнения мы пришли к двум эквивалентным решениям дифференциального уравнения, которые могут быть записанным в тригонометрической форме:

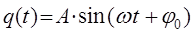
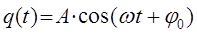
здесь величина 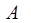есть амплитуда колебания, характеризующая размах колебательного движения, величину смещения материальной точки от положения равновесия. Аргумент 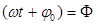называется фазой колебания, а 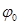- начальной фазой колебания в момент времени 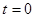. Среди различных видов колебательного движения, гармонические колебания являются наиболее простыми. Необходимо отметить, что поскольку величина 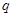характеризует смещение материальной точки от положения равновесия, а величина 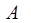- амплитуду колебательного движения (размах колебания), тогда при условии:

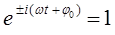
величина 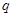будет сводиться к величине, 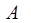и будет характеризовать, таким образом, максимальное отклонение колеблющейся материальной точки от положения равновесия, т.е. будет справедливо уравнение вида:

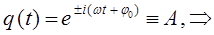и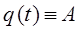

Для дальнейших выкладок рассмотрим более сложный случай – волновой процесс. Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом. При распространении волны, частицы среды не передвигаются вместе с волной, а колеблются около положений своих равновесий. При этом вместе с волной от частицы к частице среды передаётся лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы – является перенос энергии в отсутствии переноса вещества. Можно выделить следующие типы волн: волны на поверхности жидкости, упругие (механические) волны и электромагнитные волны. Упругие волны бывают продольными и поперечными. Если частицы колеблются по той же прямой, вдоль которой распространяется колебание, то такая волна называется продольной; если колебания частиц перпендикулярны к направлению распространения колебаний, то волна называется поперечной. Таким образом, продольные волны могут распространяться лишь в том случае, если в среде возникают силы упругости при деформации сжатия и растяжения. Если же при сдвиге одного слоя среды по отношению к другому слою возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия, то в среде могут распространяться поперечные волны. Если такие силы в среде не возникают, то поперечные волны образоваться не могут. Являются ли волны, распространяющиеся в среде, продольными или поперечными – зависит от упругих свойств среды. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны 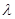. Длина волны равна тому расстоянию, на которое распространяется данная фаза колебания за период 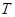. Имеем соответственно: