Вычисление ИХ по РУ (3.4а)

n	h(n), рассчитанная по (3.4а)

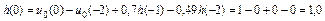
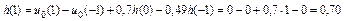
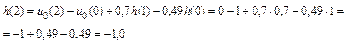
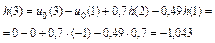
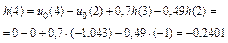
7. Результаты вычислений ИХ двумя способами в пп. 5, 6 совпадают.

8. График ИХ (5 отсчетов) представлен на рис. 3.6.

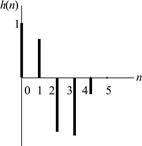
Рис. 3.6. Импульсная характеристика (к примеру 3.2)

9. Для построения карты нулей и полюсов необходимо вычислить нули и полюсы ПФ (3.1) по методике, приведенной в п. 1.4.6.

Комплексно-сопряженные полюсы, вычисленные в примере 3.1, п.4, равны

.

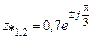Для определения нулей умножим числитель и знаменатель ПФ (3.1а) на 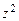, получим

,

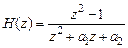и найдем корни числителя

; ; ,

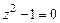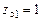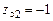которые являются вещественными нулями.

Карта нулей и полюсов изображена на рис. 3.7а; та же карта с необходимыми комментариями приведена на рис. 3.7б.

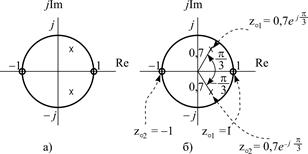
Рис. 3.7. Карта нулей и полюсов (к примеру 3.2)

10. См. п. 10 в примере 3.1.

11. Качественный анализ АЧХ и ФЧХ по карте нулей и полюсов выполняется на основе методики, изложенной в пп. 1.5.5–1.5.6.

В данном случае карта нулей и полюсов содержит два комплексно-сопряженных полюса (таких же, как в примере 3.1) и два нуля, лежащих на единичной окружности на границах основной полосы частот, поэтому относительно АЧХ можно сделать следующие выводы.

В основной полосе частот 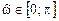АЧХ звена 2-го порядка (3.5а) является непрерывной функцией, при этом:

- внутри основной полосы частот АЧХ имеет один максимум, расположенный приблизительно на частоте полюса ;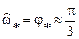

- внутри основной полосы частот АЧХ не имеет минимума;

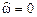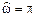- на границах основной полосы частот и АЧХ равна нулю; нули АЧХ не являются ее минимумами.

Относительно ФЧХ можно сказать, что она представляет собой непрерывную функцию, имеющую на границах основной полосы скачки на p.

12. Экспресс-анализ АЧХ и ФЧХ выполняется по методике п. 1.5.5.

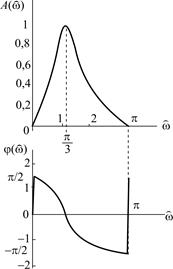
Рис. 3.8. Графики нормированной АЧХ и ФЧХ (к примеру 3.2)

В данном примере следует вычислить значения АЧХ и ФЧХ в двух точках:

а) в точке 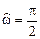при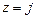

;

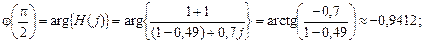
б) в точке максимума АЧХ 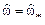, который находится приблизительно на частоте 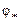полюса

; .

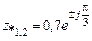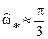Значения АЧХ и ФЧХ в этой точке, вычисленные по формулам (1.81)–(1.82), равны:

; .

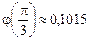13. Графики нормированной АЧХ и ФЧХ, построенные на основе качественного анализа и экспресс-анализа, представлены на рис. 3.8.

Пример 3.3.Вариант 0С (табл. 2.1, внизу).

Исходные данные – коэффициенты ПФ 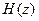2-го порядка: