Равномерная сходимость степенного ряда

Теорема: 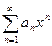равномерно сходится на любом отрезке от 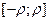целиком лежащем внутри интервала сходимости.

Доказательство:

Степенной ряд 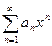сходится в точке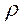 сходится числовой ряд

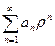
Возьмем 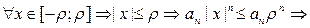степенной ряд 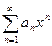мажорируется на 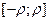сходящимся числовым рядом по признаку Вейерштрасса о равномерной сходимости степенного ряда, равномерно сходится на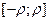

Конец доказательства.

Следствия:

1) Т.к члены степенного ряда являются непрерывными функциями, то внутри интервала сходимости сумма ряда тоже будет тоже непрерывной функцией.

2)Степенной ряд можно почленно интегрировать на любом лежащем внутри интервала сходимости.

3) Степенной ряд можно почленно дифференцировать внутри интервала сходимости, т.к интервал сходимости ряда из производных будет точно таким же.

Доказательство:

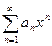- степенной ряд.

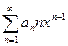- ряд из производных.

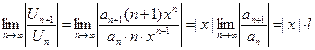
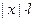<1 у ряда из производных тот же интервал сходимости.

Конец доказательства.