Равномерная сходимость функционального ряда

Определение:Функциональный ряд 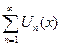называется мажорируемым на [a;b], если существует сходящийся числовой ряд из 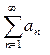, так что 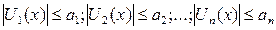…при . При 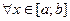этом числовой ряд 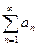- мажоранта функционального ряда .

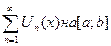Пример: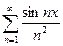

Как и числовой ряд ряд функциональный может быть записан в ви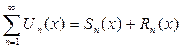де:

; где 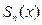- n частичная сумма ряда, 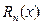- n остаток ряда.

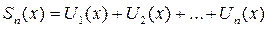
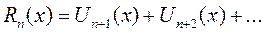
Определение: 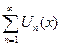называется равномерно сходящимся на [a;b], если 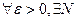начиная с которого выполняется неравенство 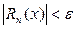, при любом 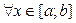, т.е 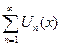- равномерно сходится на [a;b] если 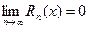, для .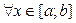

Замечание: существуют сходящиеся функциональные ряды, которые не сходятся равномерно.