Степенные ряды
Определение:Степенным рядом называется ряд вида 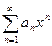 , где
, где 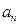 - коэффициент степенного ряда, зависит от n и не зависит от х.
- коэффициент степенного ряда, зависит от n и не зависит от х.
Степенной ряд является частным случаем функционального ряда, поэтому естественно поставить вопрос об области сходимости степенного ряда и его равномерной сходимости. Ответ на вопрос какой вид имеет область сходимости степенного ряда дает теорема Абеля.
Теорема Абеля:
Если 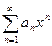 сходится в точке
сходится в точке 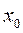
 он сходится во всех точках, удовлетворяющих неравенству
он сходится во всех точках, удовлетворяющих неравенству 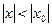 . Если
. Если 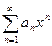 расходится в точке
расходится в точке 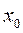
 он расходится во всех точках, удовлетворяющих неравенству
он расходится во всех точках, удовлетворяющих неравенству 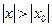 .
.
Доказательство:
Пусть 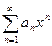 сходится в точке
сходится в точке 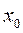
 будет сходится ряд
будет сходится ряд 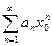
 по необходимому признаку сходимости
по необходимому признаку сходимости 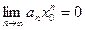
 числовая последовательность
числовая последовательность 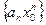 - ограничена, т.е существует число M>0, что
- ограничена, т.е существует число M>0, что 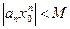 сразу для всех n.
сразу для всех n.
Возьмем любое х удовл. 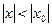 и рассмотрим
и рассмотрим 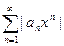 из абсолютных величин.
из абсолютных величин.
Оценим общий член этого ряда: 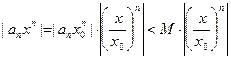
Ряд из членов геометрической прогрессии 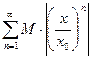 со знаменателем
со знаменателем 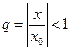 сходится
сходится  исходный
исходный 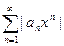 тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда
тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда 
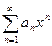 сходится абсолютно.
сходится абсолютно.
Пусть 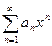 расходится в точке
расходится в точке 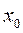 .
.
Возьмем любое х удовл. 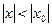 , нужно доказать, что
, нужно доказать, что 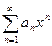 расходится при любом х, удовлетворяющем
расходится при любом х, удовлетворяющем 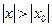 .
.
Предположим противное: 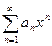 - сходится
- сходится  по 1 части доказательства он будет сходится в точке
по 1 части доказательства он будет сходится в точке 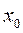 .
.
Полученное противоречие доказывает теорему.
Конец доказательства.
Из теоремы Абеля  что если степенной
что если степенной 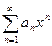 сходится в
сходится в 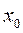
 он сходится в точке удовлетворяющей неравенству
он сходится в точке удовлетворяющей неравенству 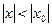 :
:
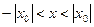
 сходится расходится
сходится расходится
расходится . .
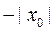 0
0 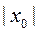
Если 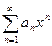 расходится в точке
расходится в точке 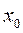 , тогда он расходится
, тогда он расходится 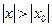
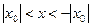
Вывод:существует интервал с центром в точке 0, радиусом R, внутри которого степенной ряд сходится, и вне которого расходится. Такой интервал называется интервалом сходимости степенного ряда, а R – радиусом сходимости степенного ряда. Укажем метод нахождения интервала сходимости.
Дата добавления: 2015-01-09; просмотров: 981;
