Условия разложимости функции в ряд Тейлора

Определение:Семейство функций 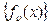называется равномерно ограниченным на множестве D, если существует число M>0, что 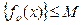сразу для всех функций семейства и любого .

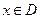Теорема:Пусть функция 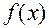-любое количество раз дифференцируема в окрестности точки 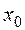и семейство ее производных любого порядка равномерно ограничено в окрестности точки 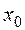,то функцию 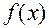можно разложить в ряд Тэйлора в окрестности точки .

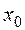Покажем что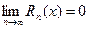

Остаточный член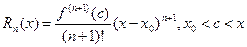

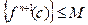, где M>0 (т.к семейство производных равномерно ограничено)

Рассмотрим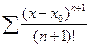

Можно показать по признаку Даламбера, что ряд сходится при любом х.

По необходимому признаку сходимости

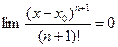
Рассмотрим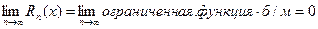

Конец доказательства.