Равномерная сетка

Эта модель описывает координаты отдельных точек поверхности следующим способом (рис. 6.11). Каждому узлу сетки с индексами (i,j) приписывается значение высоты z_i,j. Ин­дексам (i,j) соответствуют определенные значения координат (х,у). Расстояние между уз­лами одинаковое — dx по оси х и dy по оси у.

Фактически, такая модель является двумерным массивом (растром, матри­цей), каждый элемент которой хранит значение высоты.

Рис. 6.11.Узлы равномерной сетки

Рис. 6.12.Точка в сетке с координатами (x, y, z)

Не каждая поверхность может быть представлена этой моделью. Если в каж­дом узле записывается только одно зна­чение высоты, то это означает, что по­верхность описывается однозначной функцией z=f(xy). Иначе говоря, это такая поверхность, которую любая вер­тикаль пересекает только один раз. Не могут моделироваться также вертикаль­ные грани. Следует отметить, что для сетки не обязательно использовать толь­ко декартовы координаты. Например, для того, чтобы описать поверхность шара однозначной функцией, можно использо­вать полярные координаты. Равномерная сетка часто ис­пользуется для описания рельефа земной поверхности.

Рассмотрим, как можно рассчитать значение высоты для любой точки внутри границ сетки. Пусть ее координаты равняются (х, у). Надо найти соответствующее значение z. Решение этой задачи — интерполяция значений координат 2 ближайших узлов (рис 6.12).

Сначала необходимо вычислить индексы i и j одного из узлов:

где ]а[ — целая часть числа а, то есть наибольшее целое, которое не превышает а.

Далее используем, например, билинейную интерполяцию. Для этого сначала найдем значения г в точках А и В. Изпропорции

учитывая, что x_j+1 - x_j = dx, будем иметь:

Аналогично найдем

Теперь нужно вычислить такое значение z, поделив отрезок АВ пропорционально значению у:

И будем иметь: z = z_А + (y – y_i)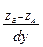

Положительные черты равномерной сетки:

1. Простота описания поверхностей

2. Возможность быстро узнать высоту любой точи поверхности простой интерполяцией.

Недостатки равномерной сетки:

1. Поверхности, которые соответствуют неоднозначной функции высоты в узлах сетки, моделироваться не могут

2. Для описания сложных поверхностей нужно большое количество узлов, которое может быть ограничено объемом памяти компьютера

3. Описание отдельных типов поверхностей может быть более сложным, чем в других моделях. Например, многогранная поверхность требует избыточный объем данных для описания в сравнении с полигональной моделью.