Аналитическая модель

Аналитической моделью будем называть описание поверхности математическими формулами. В КГ можно использовать много разновидностей такого описания. Например, в виде функции двух аргументов z = f(x, у). Можно использовать уравнение F(x, у, z) = 0.

Наиболее часто используется параметрическая форма описания поверхности. Запишем формулы для трехмерной декартовой системы координат (x, у, z):

где s и t — параметры, которые изменяются в определенном диапазоне, а функции F_x, F_y,иF_z определяют форму поверхности.

Преимущества параметрического описания — легко описывать поверхности, которые соответствуют неоднозначным функциям, замкнутые поверхности. Описание можно сде­лать таким образом, что формула не будет существенно изменяться при поворотах поверх­ности, масштабировании.

В качестве примера рассмотрим аналитическое описание поверхности шара. Сначала как функцию двух аргументов:

z = ±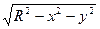

В виде уравнения: x² + y² + z² - R²=0.

А также в параметрической форме:

x=Rsins cost,y=Rsins sint, z = R coss.

Для описания сложных поверхностей часто используют сплайны. Сплайн - это специ­альная функция, наиболее пригодная для аппроксимации отдельных фрагментов поверхно­сти. Несколько сплайнов образуют модель сложной поверхности. Другими словами, сплайн — эта тоже поверхность, но такая, для которой можно достаточно просто вычислить координаты ее точек. Обычно используют кубические сплайны. Почему именно кубиче­ские? Так как третья степень является наименьшей, позволяющей описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную — такая поверхность будет без излома в местах стыка. Сплайны часто определяют параметрически. Запишем формулу для координаты x(s,t) кубического сплайна в виде многочлена третьей степени параметров s и t:

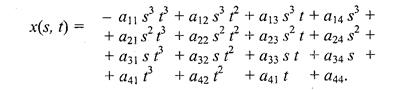
Для других координат можно записать подобные формулы — в виде функций y(s, t), z(s,t).

В математической литературе вы можете ознакомиться со способами определения ко­эффициентов a_ij для сплайнов, которые имеют заданные свойства.

Рассмотрим одну из разновидностей сплайнов — сплайн Безье. Приведем его сначала в обобщенной форме — степени тхп:

P(s,t) =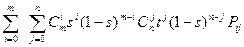

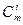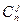где Р_ij — опорные точки-ориентиры, 0≤s≤1, 0≤t≤1, и –коэффициенты бинома Ньютона, они рассчитываются по формуле:

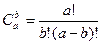
Кубический сплайн Безье соответствует т = 3, п = 3. Для его определения необходимы 16 точек-ориентиров Р_ij (рис. 6.1); коэффициенты 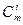и 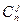равняются 1,3, 3, 1 при i,j = 0,1,2,3.

Характеризуя аналитическую модель в целом, можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхностей. С позиций КГ можно указать такие положительные черты: простота (впрочем, не всегда) расчета координат каждой точки по­верхности, нормали; небольшой объем информации для описания довольно сложных форм.

К недостаткам можно отнести: сложность формул описания с использованием функций, ко­торые медленно вычисляются в компьютере, снижают скорость выполнения операций отобра­жения; невозможность в большинстве случаев использования данной формы описания непо­средственно для построения изображения поверхности. В таких случаях поверхность обычно отображают как многогранник, используя формулы аналитического описания для расчета ко­ординат вершин граней в процессе отображения, что уменьшает скорость сравнительно с поли­гональной моделью описания.

Рис. 6.1. Кубические сплайны Безье