Показ с удалением невидимых точек

Здесь мы будем рассматривать поверхности в виде многогранников или полигональных сеток. Известны такие методы показа с удалением невидимых точек: сортировка граней по глубине, метод плавающего горизонта, метод Z-буфера и т.п.

Сортировка граней по глубине.Это означает рисование полигонов граней в порядке от самых дальних к ближним. Этот метод не является универсальным, так как иногда нельзя четко различить, какая грань ближе (рис. 6.16). Известны модификации этого метода, которые позволяют корректно рисовать подобные грани. Метод сортировки по глубине эффективен для показа поверхностей, заданных функциями z=f(x,y).

Рис. 6.16. В каком порядке рисовать грани? Поверхность нарисована четырехуголными граниями.

В общем виде алгоритм сортировки по глубине выглядит следующим образом.

Грани после разбиения сортируются по минимальному расстоянию до экранной плоскости, и выводятся в порядке их приближения (z-буфер).

Если же объекты пересекаются, то алгоритм несколько усложняется и проверяется еще ряд тестов перед выводом на экран некоторой грани P. Надо убедиться, что никакая другая грань Q не закроет P.

1. Пересекаются ли проекции граней P и любой другой Q
-на ось Ox?

-на ось Oy?

2. Пересекаются ли проекции этих граней на экранной плоскости?

3. Находится ли грань P по другую сторону плоскости, проходящей через Q, чем начало координат (наблюдатель)?

4. Обратное (2), т.е. находится ли Q по ту же сторону от плоскости, проходящей через P, что и начало координат (наблюдатель)?

Рис. 6.17. Алгоритм сортировки по глубине.

Если хотя бы один из этих тестов отрицательный, то, значит, грани упорядочены верно, и P сравнивают со следующей гранью в списке, а в противном случае грани меняют местами в списке. Для чего проверяют тесты 3. 4.

Метод плавающего горизонта.Здесь, в отличие от предыдущего метода, грани выво­дятся в последовательности от ближних к самым дальним. На каждом шаге границы граней образуют две ломаные линии — верхний горизонт и нижний горизонт. В течение вывода каждой новой грани рисуется только то, что выше верхнего горизонта, и то, что ниже ниж­него горизонта. Соответственно, каждая новая грань поднимает верхний и опускает нижний горизонты. Этот метод часто используют для показа поверхностей, которые описываются функциями z=f(x,y).

В общем виде метод выглядет следующим образом.

Пусть надо построить график функции двух переменных Z=f(x, y), в виде сетки координатных осей.

При параллельном проектировании проекций вертикальной линии является вертикальная линия.

Любая точка P(x, y, z) переходит в точку [(p_,e₁), (p, e2)] на плоскости экрана, где

e₁= (cosφ, sinφ, 0)

e₂= (sinφ, sinq, - cosφ sinq, cosq), а направление проектирования:

e₃= (sinφ cosq, - cosφ - cosq, sinq), где φє[0, 2π], qє[-π/2, π/2], - углы подобраны так, чтобы плоскость у=у₁ была ближе к экранной плоскости, чем у=у₂, т.е. у₁<у₂.

Из этого следует, что линия Z=f(x, y_j), не закрывает линию Z=f(x, y_i).

Тогда возможен алгоритм, когда линии рисуются в порядке удаления (возрастания у) и при рисовании очередной линии рисуется только та ее часть, которая не закрывается ранее нарисованной.

Для определения частей линий Z=f(x, y_к), которые не закрываются ранее нарисованными, вводятся линии горизонта.

Пусть проекцией линии Z=f(x, y_к) на плоскость экрана является линия у=у_к(х), где (х, у) – это координаты на экране. Тогда линии горизонта определяются как:

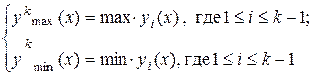
На экране рисуются только те части линии у=у^к(х), которые выше у^к_max(х) или ниже у^к_min(х).

Проще всего этот метод реализовать с помощью модифицированного растрового алгоритма Брезенхейма, который перед выводом очередного пикселя сравнивает его ординату с верхней и нижней линией (массивы ординат).

Аналогичным методом можно воспользоваться при построении объемных предметов. Только в этом случае изображение выводится по мере удаления от экранной плоскости, а по мере – приближения, т.е. начиная с дальних граней, и, заканчивая ближними, которые будут закрывать собой невидимые части более дальних граней.

Для определения порядка вывода граней считают, что грань, лежащая в полосе не может закрыть грань из полосы

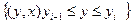
Метод Z-буфера.Здесь используется специальный дополнительный массив (буфер), в который записывается координата Z для каждого пиксела растра изображения. Координата Z означает расстояние соответствующей точки объекта до плоскости проецирования — это может быть, например, видовая координата Z (ось Z располагается перпендикулярно плос­кости проецирования).

Рассмотрим алгоритм рисования объектов в соответствии с этим методом. Пусть, чем ближе точка в пространстве к плоскости проецирования, тем больше значение Z. Тогда сна­чала Z-буфер заполняется минимальными значениями. Потом начинается вывод всех объ­емов. Причем, не имеет значения порядок вывода объектов. Для каждого объекта выводят­ся все го пикселы в любом порядке. Во время вывода каждого пиксела по его координатам (X,Y) находится текущее значение Z в Z-буфе_Ре. Если рисуемый пиксел имеет большее зна­чение Z, чем значение в Z-буфере, то этот пиксел действительно рисуется, а его Z-координата записывается в Z-буфер. Таким образом, после рисования всех пикселов всех объектов растровое изображение будет состоять из пикселов, которые соответствуют точ­кам объектов с наибольшими значениями координат Z, то есть видимые точки являются ближайшими к нам.

Метод Z-буфера сейчас очень популярен благодаря простоте и эффективности. Совре­менные ЗD-акселераторы аппаратно поддерживают этот метод как на уровне операции, так и памяти. Видеоадаптер имеет собственную память для Z-буфера, доступ к которой осуще­ствляется быстрее, чем к оперативной памяти компьютера. В конвейере графического про­цессора и манипуляции со значениями Z-буфера легко совместить с другими пиксельными операциями для вывода полигонов. Существует разновидность этого метода - для ускоре­ния вычислений используется не Z, а обратное значение (W-буфер).

Укажем некоторые проблемы использования метода Z-буфера.

1. Необходимость выделения дополнительной памяти. Для Z-буфера необходима память объем которой соответствует размерам растра изображения и точности чтения координаты Z. Используют обычно 32, 24 или 16 битов на один пиксел Z-буфера. Например для Z-буфера 1024x768x32 нужно 3 Мбайта. Сейчас такие затраты памяти не
считаются существенными. Если объем памяти _ критичен, то кадровый и Z-буфер разделяют на фрагменты (тайлы) и выполняют визуализацию для любого фрагмента отдельно. Файловая организация Z-буфера может использоваться также и для повышения скорости визуализации.

2. Полная инициализация Z-буфера (запись "самых дальних" значений) перед началом вывода того кадра уменьшает скорость анимации. Тем не менее, часто используется та­кой прием - инициализировать Z-буфер один раз для пары кадров. Это возможно, если разделить полный диапазон значений Z пополам. Например, если полный диапазон зна­чений от 0 до 1, то в первом кадре работать со значениями Z, смещенными в интервал от 1 до 0.5 (дальняя половина), а в следующем кадре — от 0.5 до 0 (ближняя половина). Однако за повышение скорости здесь приходится платить точностью вычисления глуби­ны -она уменьшается вдвое.

3. Большое количество лишних операций. Поскольку видимость устанавливается на уров­не пикселов, то в цикле выполняются лишние операции для тех полигонов, которые полностью невидимы. Такие полигоны желательно отсекать до цикла вывода. Для ускорения вывода насыщенных сцен, содержащих миллионы полигонов, известны модифи­кации метода, например, иерархический Z-буфер, в котором используется пирамида 2-х буферов разной разрешающей способности.

4. Проблемы с выводом полупрозрачных объектов.

5. Использовать в качестве расстояния координату 2 нельзя при углах обзора 180 градусов и больше. Для цилиндрических и сферических проекций лучше использовать радиаль­ное расстояние от текущей точки объекта до точки схода лучей проецирования.

Несмотря на кажущуюся простоту, эта задача является достаточно сложной. Существует 2 основных подхода к решению задачи:

первый – заключается в определении точек объекта (пикселей), которые вдоль направления проектирования ближе всего расположены к картинной плоскости;

второй – заключается в непосредственном сравнении объектов друг с другом для выяснения видимых частей.

Существует много смешанных методов, которые объединяют оба эти подхода.

Отсечение нелицевых граней

Пусть для каждой грани объекта задан единичный вектор внешней нормали 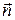, а вектор 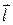- задает направление проектирования. Если нормаль грани 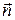с вектором 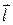составляет тупой угол, то эта грань заведомо не может быть видна.

При параллельном проектировании: это можно записать как скалярное произведение .

Рис. 6.18. Лицевые и

нелицевые грани

При центральном проектировании : с центром в точке Е, для любой точки Р вектор проектирования , а для определения, является ли грань лицевой или нет? Достаточно взять любую точку Р на ней и проверить условие . Знак этого скалярного произведения не зависит от выбора точки грани, а определяется тем, в каком полупространстве относительно плоскости, содержащей данную грань, лежит центр проектирования.

Если строится только один выпуклый многогранник, то задача может быть решена этим способом.

Если строится комбинация объектов, то используя этот подход можно хотя бы сократить вдвое количество рассматриваемых граней.

Алгоритм:

1 – сначала отбрасываются все ребра, обе грани которых не являются лицевыми, т.е. они заведомо невидны.

2 – проверяются все оставшиеся ребра со всеми гранями многоугольника на закрывание:

- грань не закрывает ребро и оно выводится.

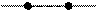- грань полностью закрывает ребро и оно удаляется из списка рассматриваемых.

- грань частично закрывает ребро, тогда ребро разбивается на части, из которых видимыми могут быть не более двух частей. Само ребро удаляется из списка, но в список проверенных ребер добавляются те его части, которые не закрываются гранью.

Алгоритм можно значительно сократить (имеем в виду количество проверок) если экранную плоскость разбить на клетки, и для каждой клетки составить список граней, проекции которых имеют непустое пересечение с этой клеткой.

Тогда для произвольного ребра сначала находятся все клетки, в которые попадает проекция этого ребра, и, следовательно, рассматриваются не все грани, а только те, которые содержатся в списке данных клеток.

При этом подходе требуется время для разбиения и составления списка, но алгоритм работает эффективней.

Рис. 6.19. Контурная линия

Здесь вводится понятие количественной невидимости, как количество граней, закрывающих вершину (точку).

Если количественная невидимость равна нулю, то точка видима.

Количественная невидимость точек ребра при прохождении так называемой контурной линии может изменяться.

Берется какая-нибудь вершина и прослеживается изменение количественной невидимости вдоль каждого из ребер, выходящих из этой вершины. Эти ребра проверяются на прохождение позади контурной линии. Где количественная невидимость равна нулю, ребро сразу рисуется. Если не равно нулю, то проверяется количественная невидимость для всех ребер, выходящих из новой вершины, и. т. д.

Этот алгоритм более эффективен, чем алгоритм Робертса, так как количество ребер, входящих в контурную линию, намного меньше общего числа ребер.

Методы двоичного разбиения пространства.

Пусть некоторая плоскость в объектном пространстве разбивает множество всех граней на два не пересекающихся множества (кластера) по одну и по другую сторону от этой плоскости.

При этом очевидно, что ни одна из этих граней, лежащих в пространстве, не содержащем наблюдателя, не может закрыть собой грань, находящуюся в другом полупространстве (где наблюдатель).

Сначала выводятся грани из дальнего кластера, затем из ближнего.

Разбиение продолжается до тех пор, пока в каждом кластере не останется по одной грани.

Обычно в качестве разбивающей плоскости рассматривают плоскость, проходящую через одну из граней. При этом реально множество граней разбивается не на 2 части, а на 4:

- грань лежит на плоскости;

- пересекает плоскость;

- в положительном пространстве;

- в отрицательной области;

Каждый узел дерева разбиения граней можно представить структурой.

Процесс построения дерева заключается в выборе грани, проведении через нее плоскости и разбиение всех граней. В процессе выбора граней следует придерживаться 2 критериев:

- получить более сбалансированное дерево;

- минимизировать количество разбиений.

Эти критерии взаимоисключающие - и надо выбрать компромисс.

Преимущество этого метода - полная независимость от положения центра проектирования, что необходимо при построении изображений одной сцены, но с разных точек наблюдения.