Уравнение в полных дифференциалах.

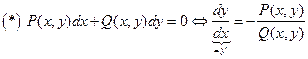
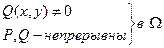
Опред.:Уравнением в полных дифференциалах называется уравнение вида 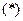, левая часть которого - полный дифференциал от некоторой функции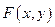

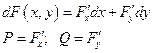
Теорема: Всякое решение уравнения в полных дифференциалах удовлетворяет уравнению 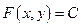для некоторого .

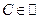Доказательство: Пусть 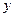- решение, 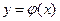- решение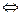

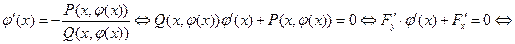
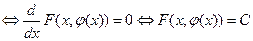. Теорема доказана.

Теорема:

Пусть функции 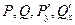непрерывны в 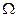. Тогда для того, чтобы уравнение 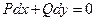было уравнением в полных дифференциалах, необходимо и достаточно условие .

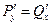Доказательство: