Динамическое программирование. Принцип оптимальности и функциональности. Функциональное уравнение Беллмана
Теории управления – развивающаяся область современной математики. Ей посвящена обширная литература , в которой исследуются различные типы управленческих систем. Рассмотрим классический метод оптимизации процесса управления, разработанный Р. Беллманом.
Пусть экономический процесс управляемый, т. е. возможно влияние на ход его развития.
Под управлением понимается совокупность решений, принимаемых на каждом этапе развития экономического процесса и направленных на его оптимизацию.
Примерами управляемых процессов являются распределение средств между предприятиями, использование ресурсов в течение ряда лет, замена оборудования, пополнение запасов и др.
Динамическое программирование (ДП) – раздел математического программирования, в котором процесс принятия решений и управления является многошаговым.
Схема процесса принятия решений методом ДП представлена на рис. 5

Рис. 5
В результате управления экономическая система S переводится из начального состояния 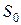 в конечное состояние
в конечное состояние 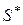 . Процесс разбит на n шагов, на каждом из которых принимается решение (управление)
. Процесс разбит на n шагов, на каждом из которых принимается решение (управление) 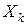 ,
, 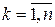 .
.
Состояние 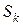 системы S в конце k-го шага зависит лишь от предшествующего состояния
системы S в конце k-го шага зависит лишь от предшествующего состояния 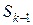 и управления
и управления 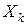 и не зависит от остальных предшествующих состояний и управлений. Такое требование называется в теории управления Беллмана условием отсутствия последействия, согласно которому уравнения состояний
и не зависит от остальных предшествующих состояний и управлений. Такое требование называется в теории управления Беллмана условием отсутствия последействия, согласно которому уравнения состояний 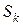 имеют вид:
имеют вид:
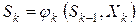 ,
, 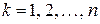 . (37)
. (37)
Обозначим показатель эффективности (оптимальности) k-го шага через
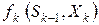 ,
, 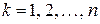 .
.
Тогда согласно еще одному требованию в теории управления Беллмана, называемому условием аддитивности, целевая функция имеет вид
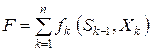 (38)
(38)
Таким образом, задача ДП (ЗДП) формулируется так: найти такое управление 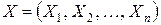 , переводящее систему S из состояния
, переводящее систему S из состояния 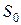 в состояние
в состояние 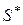 , при котором целевая функция (38) принимает экстремальное значение.
, при котором целевая функция (38) принимает экстремальное значение.
Сформулируем принцип оптимальности Беллмана:
Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге и оптимальный выигрыш на всех последующих шагах был максимальным.
Рассмотрим n-ый шаг. По принципу оптимальности 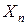 нужно выбрать так, чтобы для любых состояний
нужно выбрать так, чтобы для любых состояний 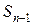 получить экстремум (для определенности возьмем максимум) целевой функции на этом шаге. Обозначим
получить экстремум (для определенности возьмем максимум) целевой функции на этом шаге. Обозначим
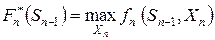 (39)
(39)
Решение 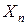 , при котором достигается
, при котором достигается 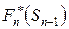 , также зависит от
, также зависит от 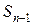 и называется условно-оптимальным управлением на n-ом шаге. Обозначим его через
и называется условно-оптимальным управлением на n-ом шаге. Обозначим его через 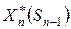 .
.
Для остальных шагов по принципу оптимальности
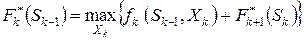 ,
, 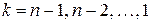 (40)
(40)
Уравнения (39) и (40) называют функциональными уравнениями Беллмана. Они по сути рекуррентные соотношения, позволяющие найти предыдущее значение функции, зная последующие.
Рассмотрим решение конкретных ЗДП.
Пример 1. Задача оптимального распределения оборудования.
Производственное объединение распределяет средства в четыре дочерние фирмы на покупку пяти производственных линий. Эксплуатация производственной линии в дочерней фирме под номером 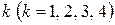 в зависимости от количества выделенных этой дочерней фирме линий
в зависимости от количества выделенных этой дочерней фирме линий 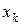 приносят прибыль
приносят прибыль 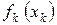 . Функции
. Функции 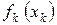 заданы таблицей 3.
заданы таблицей 3.
Таблица 3
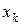
| 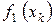
| 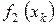
| 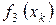
| 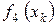
|
Найти, какое количество производственных линий нужно выделить каждой дочерней фирме, чтобы суммарная прибыль была максимальной.
Решение. Примем следующие обозначения:
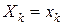 – количество производственных линий, выделяемых дочерней фирме под номером
– количество производственных линий, выделяемых дочерней фирме под номером 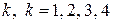 ;
;
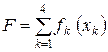 – суммарная прибыль, получаемая от эксплуатации производственных линий в четырех дочерних фирмах;
– суммарная прибыль, получаемая от эксплуатации производственных линий в четырех дочерних фирмах;
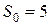 – начальное состояние системы, т. е. наличие производственных линий до начала их распределения по фирмам;
– начальное состояние системы, т. е. наличие производственных линий до начала их распределения по фирмам;
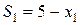 – состояние системы после первого шага, когда первой фирме выделили
– состояние системы после первого шага, когда первой фирме выделили 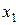 производственных линий;
производственных линий;
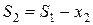 – состояние системы после второго шага, когда второй фирме выделили
– состояние системы после второго шага, когда второй фирме выделили 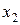 производственных линий;
производственных линий;
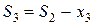 – состояние системы после третьего шага, когда третьей фирме выделили
– состояние системы после третьего шага, когда третьей фирме выделили 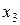 производственных линий;
производственных линий;
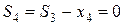 – состояние системы после четвертого шага, когда четвертой фирме выделили
– состояние системы после четвертого шага, когда четвертой фирме выделили 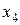 производственных линий.
производственных линий.
ЭММ задачи примет вид
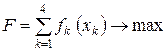
при условиях
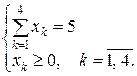
Отметим, что заданные функции 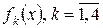 , заменяют показатели эффективности k-го шага
, заменяют показатели эффективности k-го шага 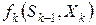 , содержащиеся в функциональных уравнениях Беллмана (39) и (40), т. е.
, содержащиеся в функциональных уравнениях Беллмана (39) и (40), т. е.
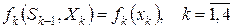 .
.
Результаты анализа возможных размещений производственных линий сведены в таблицу 4.
Первая строка нулевая (нет производственных линий, следовательно, нет прибыли).
В столбец 1 внесены возможные распределения линий 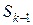 в конце
в конце 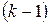 -го шага, изменяющиеся от 0 до 5.
-го шага, изменяющиеся от 0 до 5.
В столбец 2 внесены возможные управления 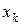 на k-ом шаге для заданного количества производственных линий
на k-ом шаге для заданного количества производственных линий 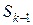
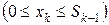 .
.
В столбец 3 внесены данные о возможных оставшихся после k-го шага количествах линий 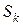 , найденные из уравнения состояния
, найденные из уравнения состояния 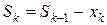 .
.
Анализ состояния системы начнем с последнего (четвертого) шага. Запишем функциональное уравнение Беллмана (39):
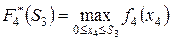 .
.
Из уравнения состояния 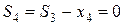 (все производственные линии распределены) находим
(все производственные линии распределены) находим 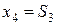 и потому
и потому
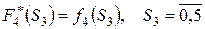 .
.
Переходим к третьему шагу. Запишем функциональное уравнение Беллмана (40):
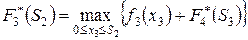 .
.
Пусть 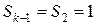 , тогда возможны два варианта:
, тогда возможны два варианта:
1) 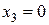 ,
, 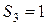
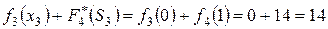 ,
,
2) 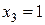 ,
, 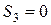
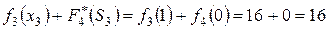 .
.
Наибольшее значение из двух полученных (14 и 16) равно 16. Следовательно, условный максимум целевой функции – 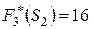 (строка 2 столбца 5), который достигается при условно оптимальном количестве производственных линий, вложенных в третью фирму, равном 1, т. е.
(строка 2 столбца 5), который достигается при условно оптимальном количестве производственных линий, вложенных в третью фирму, равном 1, т. е. 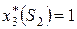 (строка 2 столбца 6).
(строка 2 столбца 6).
Аналогично проводятся расчеты для случаев 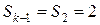 ,
, 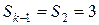 ,
, 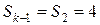 и
и 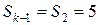 (строки 3, 4, 5 и 6 столбцов 4, 5 и 6).
(строки 3, 4, 5 и 6 столбцов 4, 5 и 6).
Второй шаг. Запишем функциональное уравнение Беллмана (14.4):
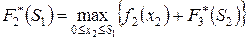 .
.
Пусть 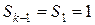 , тогда возможны два варианта:
, тогда возможны два варианта:
1) 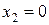 ,
, 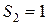
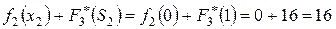 ,
,
2) 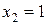 ,
, 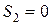
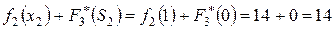 .
.
Условный максимум целевой функции – 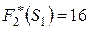 при
при 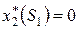 .
.
Пусть 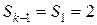 , тогда возможны три варианта:
, тогда возможны три варианта:
1) 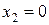 ,
, 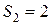
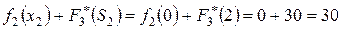 ,
,
2) 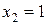 ,
, 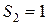
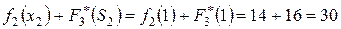 ,
,
3) 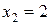 ,
, 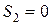
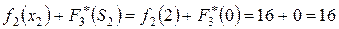 .
.
Условный максимум целевой функции – 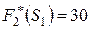 при
при 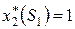 .
.
Аналогично проводятся расчеты для случаев 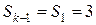 ,
, 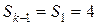 и
и 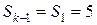 .
.
Первый шаг. Запишем функциональное уравнение Беллмана (14.4):
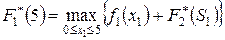 .
.
Приведем расчеты аналогично предыдущему и заполним таблицу 14.2.
В результате получим следующие выводы:
а) Максимальная прибыль от внедрения производственных линий в первую дочернюю фирму составит
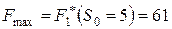 ден. ед.
ден. ед.
при оптимальном внедрении двух производственных линий 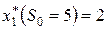 .
.
б) Оптимальное количество линий, оставшихся в конце первого шага,
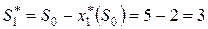
В столбце 9 таблицы 14.2 находим 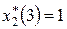 (строка 4). Оставшиеся три дочерние фирмы принесут прибыль 44 ден. ед. при вложении во вторую фирму одной линии
(строка 4). Оставшиеся три дочерние фирмы принесут прибыль 44 ден. ед. при вложении во вторую фирму одной линии 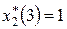 .
.
в) Оптимальное количество линий, оставшихся в конце второго шага,
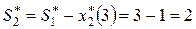
В столбце 6 таблицы 14.2 находим 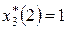 (строка 3). Оставшиеся две дочерние фирмы принесут прибыль 32 ден. ед. при вложении в третью фирму одной линии
(строка 3). Оставшиеся две дочерние фирмы принесут прибыль 32 ден. ед. при вложении в третью фирму одной линии 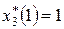 . Оставшаяся одна линия вкладывается в четвертую фирму, которая принесет прибыль 14 ден. ед.
. Оставшаяся одна линия вкладывается в четвертую фирму, которая принесет прибыль 14 ден. ед.
Ответ: оптимальное решение задачи 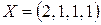 при
при 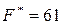 ден. ед.
ден. ед.
Таблица 4
| Номер строки | 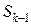
| 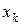
| 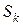
| 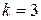
| 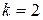
| 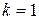
| ||||||
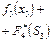
| 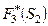
| 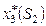
| 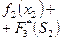
| 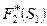
| 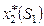
| 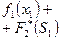
| 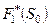
| 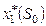
| ||||
| 0+14=14 16+0=16 | 0+16=16 14+0=14 | 0+16=16 12+0=12 | ||||||||||
| 0+15=15 16+14=30 18+0=18 | 0+30=30 14+16=30 16+0=16 | 0+30=30 12+16=28 17+0=17 | ||||||||||
| 0+18=18 16+15=31 18+14=32 21+0=21 | 0+32=32 14+30=44 16+16=32 18+0=18 | 0+44=44 12+30=42 17+16=33 20+0=20 | ||||||||||
| 0+20=20 16+18=34 18+15=33 21+14=35 24+0=24 | 0+35=35 14+32=46 16+30=46 18+16=34 20+0=20 | 0+46=46 12+44=58 17+30=47 20+16=36 22+0=22 | ||||||||||
| 0+24=24 16+20=36 18+18=36 21+15=36 24+14=38 26+0=26 | 0+38=38 14+35=49 16+32=48 18+30=48 20+16=36 24+0=24 | 0+49=49 12+46=58 17+44=61 20+30=50 22+16=38 26+0=26 |
ЛЕКЦИЯ 7
Дата добавления: 2015-02-03; просмотров: 2075;
