Модели потребительского выбора. Функция полезности. Линии безразличия. Оптимизация функции полезности. Функции спроса и предложения.
Пусть потребитель, располагая некоторой суммой средств, полностью тратит ее на приобретение товаров. Набор товаров покупает исходя из имеющейся суммы средств и собственных предпочтений. Математическая модель поведения такого потребителя называется моделью потребительского выбора.
Функция полезности
Рассмотрим потребительский набор из двух товаров ( 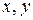 ), где x и y – количество единиц первого и второго товаров соответственно. Потребительский набор – это точка в прямоугольной системе координат xOy с координатами (
), где x и y – количество единиц первого и второго товаров соответственно. Потребительский набор – это точка в прямоугольной системе координат xOy с координатами ( 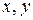 ).
).
Отношение потребителя к различным наборам товаров называют выбором потребителя.
Если каждому набору ( 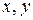 ) поставить в соответствие потребительскую оценку этого набора в виде некоторого числа u, то получим функцию полезности потребителя u(
) поставить в соответствие потребительскую оценку этого набора в виде некоторого числа u, то получим функцию полезности потребителя u( 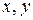 ).
).
Пусть набор 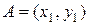 предпочтительнее набора
предпочтительнее набора 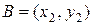 . Тогда оценка потребителем набора
. Тогда оценка потребителем набора 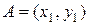 превосходит оценку набора
превосходит оценку набора 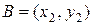 , т.е.
, т.е. 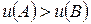 . Каждый потребитель имеет свою функцию полезности.
. Каждый потребитель имеет свою функцию полезности.
Свойства функции полезности
1. Возрастание потребления одного продукта при постоянном потреблении другого приводит к росту функции полезности:
при 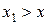 имеем
имеем 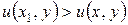 ;
;
при 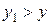 имеем
имеем 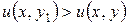 .
.
Отсюда следует
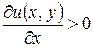 ,
, 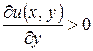 .
.
Первые частные производные от функции полезности потребителя называются предельными полезностямисоответствующих продуктов:
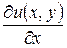 – предельная полезность первого продукта;
– предельная полезность первого продукта;
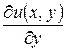 – предельная полезность второго продукта.
– предельная полезность второго продукта.
2. Функция полезности должна быть, по крайней мере, дважды дифференцируемой. Частная производная от предельной полезности продукта по той же переменной должна быть отрицательной, т.е. предельная полезность уменьшается с ростом этой переменной (этого продукта). Отсюда следует, что вторые частные производные по тому же аргументу должны быть отрицательны, т.е.
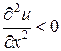 ,
, 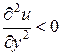 .
.
Это свойство называется законом убывания предельной полезности.
3. Вторая частная производная от предельной полезности продукта по другой переменной должна быть положительной, т.е. предельная полезность увеличивается с ростом другой переменной (другого продукта). Таким образом,
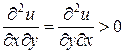 .
.
Если функция полезности в задаче потребительского выбора не обладает свойствами 2 и 3, она тем не менее может описывать реальное поведение потребителя.
Линии безразличия
Линии уровня функции полезности потребителя называются линиями безразличия.
Линии безразличия являются функциями одной переменной. Данная функция имеет вид:
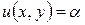 ,
,
где 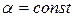 .
.
Множество линий безразличия называется картой линий безразличия (рис. 5).
На рис. 5 изображены линии безразличия, имеющие уровни полезности потребителя 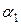 ,
, 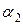 и
и 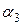 . Линии безразличия не касаются и не пересекаются. При увеличении уровня функции полезности
. Линии безразличия не касаются и не пересекаются. При увеличении уровня функции полезности 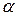 линии безразличия смещаются вправо вверх. Для примера рис. 11.1 справедливо неравенство
линии безразличия смещаются вправо вверх. Для примера рис. 11.1 справедливо неравенство 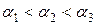 .
.
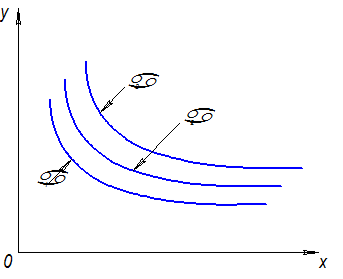
Рис. 5 Линии безразличия
Из приведенных выше свойств функции полезности следует, линия безразличия в системе координат хОу является убывающей и выпуклой вниз (вогнутой) функцией.
Если рассматривать дифференциал функции полезности 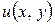 при движении вдоль линии уровня, то видно, что он равен нулю. Это связано с тем, что значение функции при этом не изменяется. Таким образом,
при движении вдоль линии уровня, то видно, что он равен нулю. Это связано с тем, что значение функции при этом не изменяется. Таким образом,
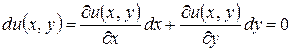 .
.
Отсюда следует, что
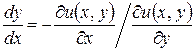 . (41)
. (41)
Производная 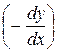 называется предельной нормой замены первого продукта вторым.
называется предельной нормой замены первого продукта вторым.
Так как числитель и знаменатель дроби – величины положительные (свойство 1), то производная функции безразличия 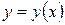 является отрицательной, т.е. данная функция является убывающей.
является отрицательной, т.е. данная функция является убывающей.
Вторая производная функции 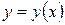 находится путем дифференцирования (41):
находится путем дифференцирования (41):
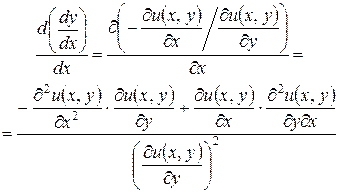 .
.
Так как первое слагаемое числителя положительно в силу свойств 1 и 2 функции полезности, второе слагаемое числителя также положительно в силу свойств 1 и 3 функции полезности, то вторая производная функции безразличия 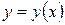 является величиной положительной. Отсюда следует, что линии безразличия выпуклы к низу.
является величиной положительной. Отсюда следует, что линии безразличия выпуклы к низу.
Если перейти от бесконечно малых приращений dx и dy к конечным приращениям 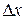 и
и 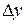 , то можно записать следующее приближенное равенство:
, то можно записать следующее приближенное равенство:
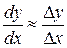 .
.
Сопоставив данное выражение с (41), найдем
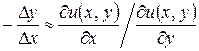 . (42)
. (42)
Дробь 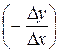 называется нормой замены первого продукта вторым.Норма замены показывает, насколько изменится потребление второго продукта при изменении потребления первого продукта на единицу. Если известна функция полезности
называется нормой замены первого продукта вторым.Норма замены показывает, насколько изменится потребление второго продукта при изменении потребления первого продукта на единицу. Если известна функция полезности 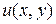 то норма замены рассчитывается по формуле (42).
то норма замены рассчитывается по формуле (42).
Пример. Пусть в течение месяца потребляется 45 единиц продукта х и 36 единиц продукта у. Функция полезности потребителя задана соотношением
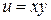 .
.
Определить величину, на которую потребитель должен увеличить потребление второго продукта при уменьшении потребления первого на десять единиц.
Решение. Норму замены первого продукта вторым находят из соотношения (42):
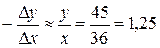
При уменьшении потребления продукта х на 10 единиц потребление продукта у возрастет на 12,5 единиц. Действительно,
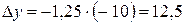
Таким образом, норма замены показывает, на сколько должен потребитель увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на заданную величину.
Оптимизация функции полезности
Естественно, что потребитель желает так использовать имеющиеся у него средства, чтобы получить максимальную пользу при затрате некоторого заданного их количества.
Задачей потребительского выбора называется определение такого потребительского набора, который максимизирует функцию полезности потребителя при заданном бюджетном ограничении. Этот набор называют оптимальным для потребителя, или локальным рыночным равновесием потребителя.
Бюджетным ограничением называется денежная сумма (доход), предназначенная на покупку данного набора товаров.
Если товаров два, то бюджетное ограничение I и цены на первый 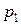 и второй
и второй 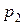 товары связаны соотношением
товары связаны соотношением
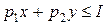 . (43)
. (43)
Задачу математического выбора можно записать в виде ЗМП:
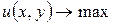
при условиях
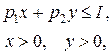 (44)
(44)
При решении задачи математического выбора (44) обычно бюджетное ограничение 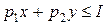 заменяют на равенство
заменяют на равенство 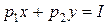 . Это связано с тем, что значение функции полезности увеличивается при увеличении x и y. Максимум лежит на крайних правых и нижних точках. Следовательно, задачу математического программирования можно заменить задачей на условный экстремум:
. Это связано с тем, что значение функции полезности увеличивается при увеличении x и y. Максимум лежит на крайних правых и нижних точках. Следовательно, задачу математического программирования можно заменить задачей на условный экстремум: 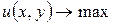 при условиях
при условиях
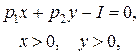 (45)
(45)
где 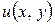 - целевая функция;
- целевая функция; 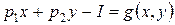 – функция связи.
– функция связи.
Функция Лагранжа для этой задачи имеет вид:
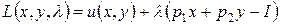 .
.
Составляем систему линейных уравнений, для чего приравниваем к нулю первые частные производные функции Лагранжа:
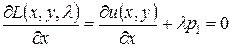 ;
;
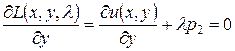 ;
;
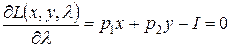 .
.
Умножим первое уравнение на 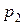 , а второе – на
, а второе – на 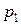 и вычтем второе уравнение из первого:
и вычтем второе уравнение из первого:
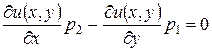 .
.
Таким образом, систему уравнений для укороченной подозрительной точки функции Лагранжа можно переписать в виде:
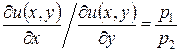 ; (46)
; (46)
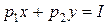 . (47)
. (47)
Сопоставив (46) с (42), получим 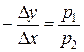 ,
,
т.е. норма замены первого продукта вторым равна отношению цены первого продукта к цене второго.
Геометрический смысл условного экстремума функции 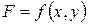 в точке
в точке 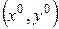 состоит в том, что градиенты целевой функции
состоит в том, что градиенты целевой функции 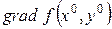 и функции связи
и функции связи 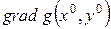 , выходящий из точки
, выходящий из точки 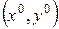 , обязательно расположены на одной прямой и перпендикулярны линиям уровней функций
, обязательно расположены на одной прямой и перпендикулярны линиям уровней функций 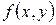 и
и 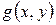 . Линией уровня функции полезности является линия безразличия, а линия уровня функции связи совпадает с бюджетной прямой. Линии уровней функций
. Линией уровня функции полезности является линия безразличия, а линия уровня функции связи совпадает с бюджетной прямой. Линии уровней функций 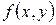 и
и 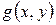 , содержащие точку
, содержащие точку 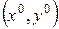 , касаются в этой точке.
, касаются в этой точке.
Градиент 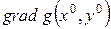 функции
функции 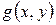 в точке
в точке 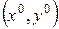 направлен вправо вверх. Действительно,
направлен вправо вверх. Действительно,
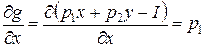 ,
, 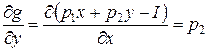 .
.
Поэтому
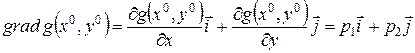 ,
,
а 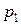 и
и 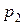 положительны по условию задачи.
положительны по условию задачи.
Точно так же направлен градиент функции 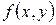
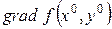 в точке
в точке 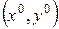 .
.
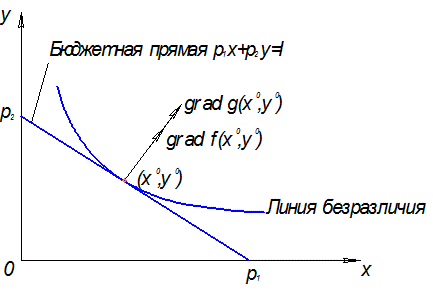
Рис. 6
ЛЕКЦИЯ 8
Дата добавления: 2015-02-03; просмотров: 2675;
