Решение матричных игр в смешанных стратегиях
Рассмотрим конечные матричные игры, в которых нет седловой точки, т.е. 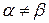 .
.
Нетрудно доказать, что 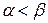 . Если игра одноходовая, то по принципу минимакса игроку А гарантирован выйгрыш
. Если игра одноходовая, то по принципу минимакса игроку А гарантирован выйгрыш 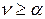 , а игроку В – проигрыш
, а игроку В – проигрыш 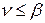 . Таким образом, для цены игры
. Таким образом, для цены игры 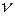 справедливо соотношение
справедливо соотношение
 (48)
(48)
Если игра повторяется неоднократно, то постоянный выбор игроками минимаксных стратегий не логичен. Действительно, игрок В, зная что игрок А применяет лишь минимаксную стратегию 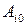 , выберет иную стратегию – стратегию, соответствующую наименьшему элементу в строке
, выберет иную стратегию – стратегию, соответствующую наименьшему элементу в строке 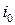 платежной матрицы. Такие же рассуждения имеют место и для поведения игрока А. Следовательно, при неоднократном повторении игры игрокам необходимо менять стратегии. Выясним механизм выбора игроками оптимальных стратегий, а также что принять за стоимость игры.
платежной матрицы. Такие же рассуждения имеют место и для поведения игрока А. Следовательно, при неоднократном повторении игры игрокам необходимо менять стратегии. Выясним механизм выбора игроками оптимальных стратегий, а также что принять за стоимость игры.
Рассмотрим матричную игру, заданную таблицей 6.
Таблица 6
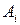
| 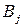
| 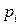
| |||
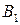
| 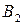
| ¼ | 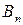
| ||
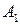
| 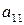
| 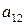
| ¼ | 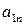
| 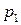
|
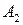
| 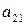
| 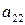
| ¼ | 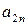
| 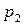
|
| ¼ | ¼ | ¼ | ¼ | ¼ | ¼ |
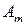
| 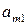
| 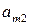
| ¼ | 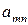
| 
|
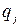
| 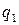
| 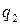
| ¼ | 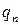
|
Через 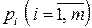 и
и 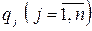 обозначим соответственно вероятности (относительные частоты), согласно которым игроки А и В выбирают стратегии
обозначим соответственно вероятности (относительные частоты), согласно которым игроки А и В выбирают стратегии 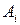 и
и 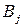 .
.
Очевидно, что 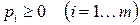 ,
, 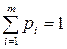 ,
,  ,
, 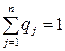 . Упорядоченные множества
. Упорядоченные множества 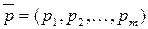 и
и 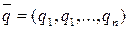 полностью определяет характер игры игроков А и В и называются их смешанными стратегиями. Отметим, что любая их чистая стратегия
полностью определяет характер игры игроков А и В и называются их смешанными стратегиями. Отметим, что любая их чистая стратегия 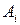 и
и 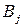 может быть описана как смешанная. Действительно,
может быть описана как смешанная. Действительно, 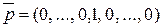 или
или 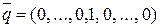 .
.
Пусть игроки А и В применяют смешанные стратегии p и q, выбирают их случайно. Тогда вероятность выбора комбинации 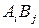 будет равна
будет равна 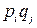 .
.
Игра приобрела случайный характер. Следовательно, случайной становится и величина выигрыша.
Этой величиной является математическое ожидание выигрыша, которое определяется формулой:
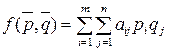
Функцию 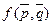 называют платежной функцией игры с заданной матрицей. Как и выше, введем понятие нижней и верхней цены игры, сохраняя при этом обозначения
называют платежной функцией игры с заданной матрицей. Как и выше, введем понятие нижней и верхней цены игры, сохраняя при этом обозначения 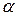 и
и 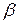 :
:
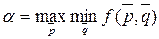 ,
, 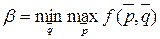 .
.
Оптимальными смешанными стратегиями 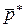 и
и 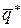 называют такие стратегии, при которых
называют такие стратегии, при которых 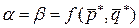 . Величину
. Величину 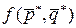 называют ценой игрыv.
называют ценой игрыv.
Для практических целей важны следующие свойства оптимальных смешанных стратегий, выражаемые следующими теоремами.
Сформулируем основную теорему теории игр.
Теорема (Нейман): Любая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.
Теорема 1. Для того чтобы смешанные стратегии 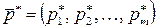 и
и 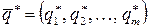 были оптимальными, необходимо и достаточно выполнение неравенств
были оптимальными, необходимо и достаточно выполнение неравенств
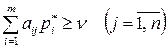 (49)
(49)
 (50)
(50)
Теорема 2. Пусть 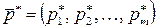 и
и 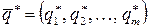 – оптимальные смешанные стратегии и
– оптимальные смешанные стратегии и 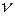 – цена игры.
– цена игры.
Только те вероятности 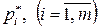 , отличны от нуля, для которых
, отличны от нуля, для которых
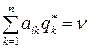 .
.
Только те вероятности 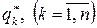 , отличны от нуля, для которых
, отличны от нуля, для которых
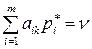 .
.
Методы решения матричных игр в смешанных стратегиях.
В этой лекции рассматриваются матричные игры, не имеющие седловых точек.
Игры.
Рассмотрим игру с платежной матрицей
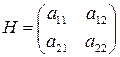
Пусть игрок A применяет набор своих оптимальных стратегий 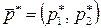 . По основной теореме теории игр это обеспечивает ему выигрыш
. По основной теореме теории игр это обеспечивает ему выигрыш 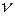 при любых стратегиях игрока В, т.е. выполняются соотношения:
при любых стратегиях игрока В, т.е. выполняются соотношения:
 (51)
(51)
Дополняя их уравнением
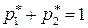 (52)
(52)
получим систему линейных уравнений относительно 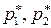 и
и 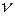 . Решая ее найдем
. Решая ее найдем
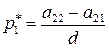 ,
, 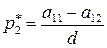 ,
, 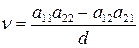 , (53)
, (53)
где 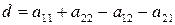 .
.
Повторяя те же рассуждения для игрока В, получим систему линейных уравнений
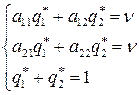 (54)
(54)
Ее решениями будут
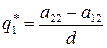 ,
, 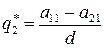 ,
, 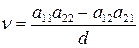 , (55)
, (55)
Пример.Молокозавод поставляет в магазин молочную продукцию (  ) и кисломолочную продукцию (
) и кисломолочную продукцию (  ). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции
). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции  в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции
в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции  в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
Решение. Примем молокозавод за игрока А, а магазин – за игрока В. Составим платежную матрицу игры:
| Сроки Продукция | 1-ый срок | 2-ой срок |
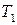
| ||
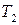
|
или
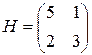
Найдем
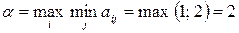
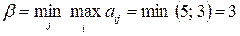 ,
,
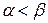 , седловой точки нет. Применим формулы (53) – (55) для определения оптимальных стратегий и цены игры:
, седловой точки нет. Применим формулы (53) – (55) для определения оптимальных стратегий и цены игры:
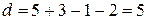 ,
, 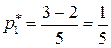 ,
,  ,
, 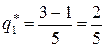 ,
,
 ,
, 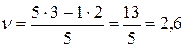 ,
,
Оптимальные стратегии:  ,
, 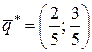 , цена игры
, цена игры 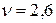 .
.
Таким образом, молокозавод поставляет молочную продукцию с вероятностью 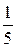 , а кисломолочную продукцию – с вероятностью
, а кисломолочную продукцию – с вероятностью 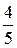 , а магазин получает продукцию в 1-ый срок с вероятностью
, а магазин получает продукцию в 1-ый срок с вероятностью 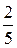 , а во 2-ой срок – с вероятностью
, а во 2-ой срок – с вероятностью 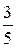 и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
Матричная игра 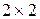 допускает простую геометрическую интерпретацию.
допускает простую геометрическую интерпретацию.
Нахождение цены игры 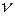 и оптимальной стратегии
и оптимальной стратегии 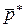 для игрока А равносильно решению уравнения:
для игрока А равносильно решению уравнения:
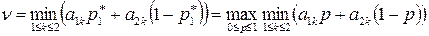 (56)
(56)
Для нахождения правой части (56) применим графический метод.
Пусть игрок А выбрал смешанную стратегию 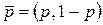 ,
, 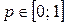 , а игрок В – k-ую чистую стратегию,
, а игрок В – k-ую чистую стратегию, 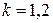 . Тогда средний выигрыш игрока А окажется равным
. Тогда средний выигрыш игрока А окажется равным
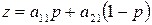 при стратегии
при стратегии 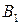 (57)
(57)
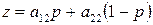 при стратегии
при стратегии 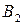 (58)
(58)
Очевидно, 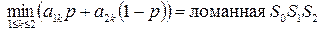 , которую называют нижней огибающей прямых I и II.
, которую называют нижней огибающей прямых I и II.
Нетрудно видеть, что 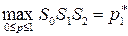
Таким образом, верхняя точка нижней огибающей – 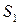 определяет оптимальную стратегию игрока А:
определяет оптимальную стратегию игрока А: 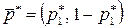 и цену игры
и цену игры 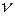 .
.
Проиллюстрируем описанный графичексий метод на рассмотренной выше игре с платежной матрицей 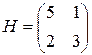 .
.
На плоскости pOz построим две прямые, описываемые уравнениями: 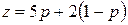 и
и 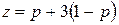 или
или 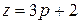 (I) и
(I) и 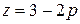 (II).
(II).
Решая систему уравнений
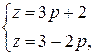
найдем 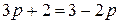 ,
, 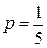 ,
, 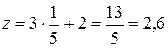 .
.
Таким образом, имеем полученный выше ответ игры:  и
и 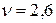 .
.
Теперь покажем как графическим методом найти стратегии игрока В.
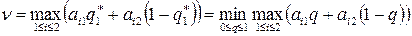 (59)
(59)
Пусть игрок В выбрал смешанную стратегию 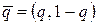 ,
,  , а игрок А – i-ую чистую стратегию,
, а игрок А – i-ую чистую стратегию, 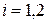 . Тогда средний выигрыш игрока В окажется равным
. Тогда средний выигрыш игрока В окажется равным
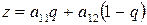 при стратегии
при стратегии 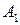 (60)
(60)
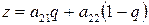 при стратегии
при стратегии 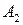 (61)
(61)
На плоскости qOz уравнения (60) и (61) описывают прямые III и IV
Очевидно,  , которую называют верхней огибающей прямых III и IV.
, которую называют верхней огибающей прямых III и IV.
Нетрудно видеть, что 
Таким образом, нижняя точка верхней огибающей – 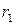 определяет оптимальную стратегию игрока В:
определяет оптимальную стратегию игрока В: 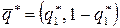 и цену игры
и цену игры 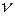 .
.
Для рассмотренной выше гры с матрицей H найдем стратегии игрока В.
На плоскости qOz построим две прямые, описываемые уравнениями:  и
и 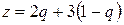 или
или 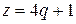 (III) и
(III) и 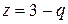 (IV).
(IV).
Решая систему уравнений

найдем  ,
, 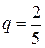 ,
, 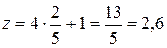 .
.
Таким образом, имеем 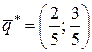 и
и 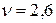 .
.
Замечания. На практике оптимальную стратегию игрока В, если оптимальная стратегия игрока А, следовательно, и цена игры известны, находят приравниванием любого из двух средних выйгрышей игрока В к цене игры:
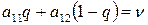 или
или 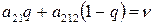 .
.
Для рассмотренного примера такими уравнениями будут
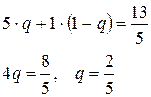 или
или 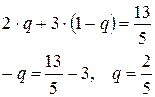
Аналогично находят оптимальную стратегию игрока А, если известна оптимальная стратегия игрока В.
Дата добавления: 2015-02-03; просмотров: 1195;
