И – игры.
Решают такие игры графическим способом, описанным выше. Отличие от 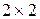 – игр заключается в следующем.
– игр заключается в следующем.
1) Нижняя (верхняя) огибающая семейства прямых
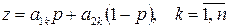
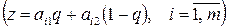
содержит большее число отрезков.
2) Пусть в игре 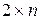 в верхней точке нижней огибающей пересекаются прямые
в верхней точке нижней огибающей пересекаются прямые 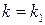 и
и 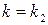 . Тогда при нахождении оптимальной смешанной стратегии игрока В согласно Теореме 2 полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока В согласно Теореме 2 полагают, что 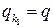 ,
, 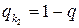 ,
, 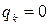 ,
, 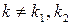 , где q – решение уравнения
, где q – решение уравнения
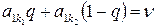 или
или 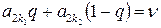
3) Пусть в игре 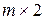 в нижней точке верхней огибающей пересекаются прямые
в нижней точке верхней огибающей пересекаются прямые 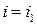 и
и 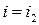 . Тогда при нахождении оптимальной смешанной стратегии игрока А согласно Теореме 2 полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока А согласно Теореме 2 полагают, что 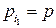 ,
, 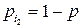 ,
, 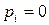 ,
, 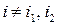 , где p – решение уравнения
, где p – решение уравнения
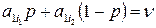 или
или 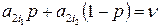 .
.
Игры.
При решении таких игр рекомендуется предварительно уменьшить размеры платежной матрицы или упростить ее в некотором смысле. С этой целью применяют следующие правила.
Правило доминировнаия.
Из платежной матрицы исключают чистые стратегии заведомо невыгодные по сравнению с другими:
а) для игрока А такими стратегиями являются те, которым соответствуют строки с элементами не большими по сравнению с элементами других строк;
б) для игрока В такими стратегиями являются те, которым соответствуют столбцы с элементами не меньшими по сравнению с элементами других столбцов.
Например, рассмотрим игру с матрицей
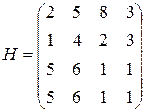
Сравнивая строки, убеждаемся, что элементы 2-ой строки не больше соответствующих элементов 1-ой строки, а 3-ья строка совпадает с 4-ой. Следовательно, стратегии 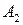 и
и 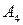 невыгодные и могут быть отброшены. Матрица игры преобразуется к матрице
невыгодные и могут быть отброшены. Матрица игры преобразуется к матрице
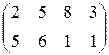
Сравнивая столбцы полученной матрицы, убеждаемся, что элементы 2-го столбца не меньше соответствующих элементов 1-го столбца, а элементы 3-го столбца не меньше соответствующих элементов 4-го столбца, т.е. стратегии 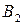 и
и 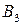 также могут быть отброшены. Окончательно усеченная матрица игры имеет вид
также могут быть отброшены. Окончательно усеченная матрица игры имеет вид
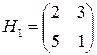 .
.
Таким образом, оптимальными стратегиями игроков А и В игры с матрицей Н будут 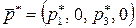 и
и 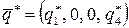 , где
, где 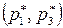 и
и 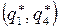 – оптимальные стратегии игры с матрицей
– оптимальные стратегии игры с матрицей 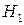 .
.
Аффинное правило.
Пусть 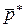 и
и 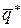 – оптимальные смешанные стратегии игроков А и В в игре с платежной матрицей
– оптимальные смешанные стратегии игроков А и В в игре с платежной матрицей 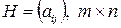 и ценой
и ценой 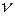 . Тогда
. Тогда 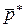 и
и 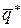 будут оптимальными стратегиями и в игре с матрицей
будут оптимальными стратегиями и в игре с матрицей 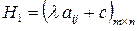 и ценой
и ценой 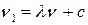 .
.
Например, игру с матрицей 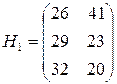 можно заменить игрой с матрицей
можно заменить игрой с матрицей 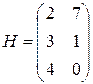 , т.к. элементы этих матриц связаны соотношениями
, т.к. элементы этих матриц связаны соотношениями 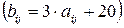 :
: 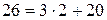 ;
; 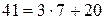 ;
; 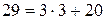 ;
; 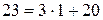 ;
; 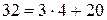 ;
; 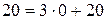 . При этом оптимальные стратегии игр совпадают, а цены игр связаны соотношением
. При этом оптимальные стратегии игр совпадают, а цены игр связаны соотношением 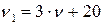 .
.
В общем случае решение игр размера 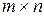 в смешанных стратегиях сводят к решению двух возможно двойственных ЗЛП. Изучению этого вопроса посвящена следующая лекция.
в смешанных стратегиях сводят к решению двух возможно двойственных ЗЛП. Изучению этого вопроса посвящена следующая лекция.
ЛЕКЦИЯ 9
Дата добавления: 2015-02-03; просмотров: 849;
