Решение матричных игр в чистых стратегиях
Пусть у игроков А и В соответственно m и n чистых стратегий, которые обозначим через 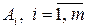 и
и 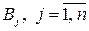 .
.
Выбор игроками любой пары стратегий 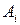 и
и 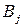 однозначно определяет исход игры, описываемый числом
однозначно определяет исход игры, описываемый числом 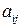 . Матрица
. Матрица 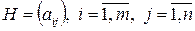 называется платежной матрицей, где
называется платежной матрицей, где 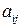 – выигрыш игрока А и проигрышь
– выигрыш игрока А и проигрышь 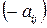 игрока В.
игрока В.
Платежную матрицу удобно также представить в виде таблицы 5
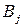
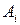
| 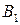
| 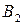
| ¼ | 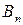
|
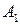
| 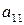
| 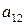
| ¼ | 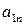
|
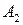
| 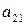
| 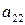
| ¼ | 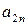
|
| ¼ | ¼ | ¼ | ¼ | ¼ |
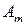
| 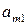
| 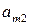
| ¼ | 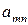
|
В ее строках расположены чистые стратегии игрока А, а в столбцах – чистые стратегии игрока В.
Цель матричной игры – выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В – минимальный проигрыш. Стратегию игрока А называют оптимальной, если при ее применении выигрыш игрока А не уменьшается при любой стратегии игрока В. Оптимальной для игрока В называют стратегию, при которой проигрыш игрока В не увеличивается при любой стратегии игрока А. При поиске оптимальных стратегий игроки соблюдают принцип осторожности, согласно которому противник является по меньшей мере таким же разумным и не упустит ни единой возможности использовать любую ошибку соперника в своих интересах. Пусть игрок А выбрал некоторую стартегию 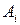 . Сначала он найдет минимальное значение ожидаемого выигрыша:
. Сначала он найдет минимальное значение ожидаемого выигрыша: 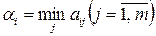 , а затем из всех
, а затем из всех 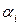 выберет наибольшее
выберет наибольшее 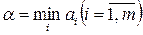 .
.
Число a называют нижней ценой игры и является гарантированным выигрышем игрока А.
Очевидно, a находится в одной из строк матрицы H, к примеру в строке 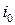 . Тогда стратегию
. Тогда стратегию 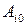 называют максиминной, т.к.
называют максиминной, т.к. 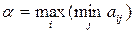 .
.
В свою очередь игрок В, стремясь минимизировать проигрыш и используя принцип осторожности, сначала для каждой чистой стратегии 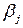 найдет максимально возможный проигрыш –
найдет максимально возможный проигрыш – 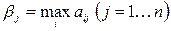 , а затем среди
, а затем среди 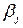 выберт минимальное значение
выберт минимальное значение 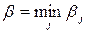 . Ему будет соответствовать чистая стратегия
. Ему будет соответствовать чистая стратегия 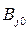 , называемая минимаксной, т.к.
, называемая минимаксной, т.к. 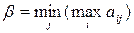 . Число
. Число 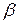 называют верхней ценой игры. Оно показывает какой максимальный проигрыш может быть у игрока В. Таким образом, правильно используя чистые стратегии, игрок А обеспечит выигрыш не меньше a, а игрок В не позволит игроку А выиграть больше чем b.
называют верхней ценой игры. Оно показывает какой максимальный проигрыш может быть у игрока В. Таким образом, правильно используя чистые стратегии, игрок А обеспечит выигрыш не меньше a, а игрок В не позволит игроку А выиграть больше чем b.
Рассмотрим примеры нахождения 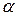 и
и 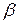 .
.
Пример 1. Пусть игра задана платежной матрицей  :
:
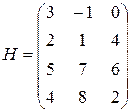
Выпишем для каждой строки справа от матрицы  , а снизу
, а снизу 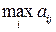 каждого столбца. Тогда получим
каждого столбца. Тогда получим
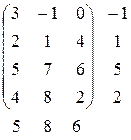
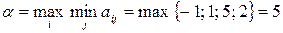
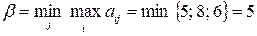
Верхняя и нижняя цены игры совпали: 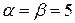 .
.
Пример 2. Задана платежная матрица
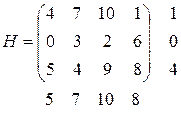
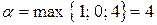
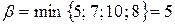
Здесь 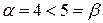 .
.
Теорема 1. В любой матричной игре нижняя цена игры не превосходит верхней цены игры, т.е. 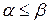 .
.
Обозначим через 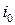 и
и 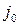 номера чистых стратегий, при котором
номера чистых стратегий, при котором 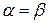 . Пару чистых стратегий
. Пару чистых стратегий 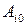 и
и 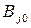 при этом называют седловой точкой игры, а
при этом называют седловой точкой игры, а 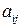 – седловым элементом платежной матрицы.
– седловым элементом платежной матрицы.
Число 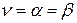 называют чистой ценой игры. Простота решения игры с седловой точкой заключается в том, что сразу найдены оптимальные стратегии: максиминная
называют чистой ценой игры. Простота решения игры с седловой точкой заключается в том, что сразу найдены оптимальные стратегии: максиминная 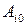 для игрока А и минимаксная
для игрока А и минимаксная 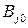 для игрока В, а цена игры – седловой элемент платежной матрицы:
для игрока В, а цена игры – седловой элемент платежной матрицы: 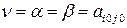 . Отметим, что матричная игра может содержать несколько седловых точек. Максиминные и минимаксные стратегии называют общим термином – минимаксными стратегиями, а их выбор – принципом минимакса.
. Отметим, что матричная игра может содержать несколько седловых точек. Максиминные и минимаксные стратегии называют общим термином – минимаксными стратегиями, а их выбор – принципом минимакса.
Дата добавления: 2015-02-03; просмотров: 1436;
