Метод искусственного базиса (М-метод).
Применительно к рассматриваемой задаче М-метод заключается в следующем. В каждое уравнение системы ограничений (6.11), введем свою новую искусственную неизвестную: 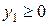 ,
, 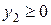 и
и 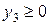 . Включим их в число базисных неизвестных и составим новую функцию цели
. Включим их в число базисных неизвестных и составим новую функцию цели
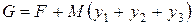 ,
,
где М – произвольно большое положительное число.
В результате получили следующую ЗЛП, приведенную к допустимому виду
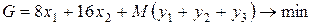
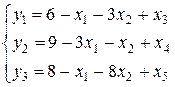
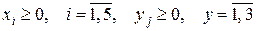 .
.
Эту задачу называют М-задачей.
Сформулируем утверждения, устанавливающие связь между решениями исходной задачи и М-задачи.
1. Если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. 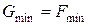 , если
, если 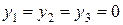 ).
).
2. Если имеется оптимальное решение М-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то исходная задача не имеет допустимого решения.
3. Если М-задача не имеет оптимального решения, то исходная задача неразрешима (т.е. если 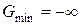 , то либо
, то либо 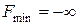 , либо нет ни одного допустимого решения).
, либо нет ни одного допустимого решения).
Из этих утверждений следует следующее правило решения M-задачи симплекс-методом:
а) Необходимо выбирать последовательность шагов таким образом, чтобы все искусственные неизвестные 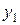 ,
, 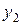 ,
, 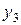 вышли из базиса, т.е. стали свободными.
вышли из базиса, т.е. стали свободными.
б) В симплекс-таблице отбросив столбцы для этих неизвестных, получим симплекс-таблицу, дающую оптимальное решение исходной задачи.
в) Если при решении М-задачи получена симплекс-таблица, дающее оптимальное решение, и в этой таблице хотя бы одна искусственная переменная 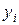 входит в базис, причем в строке для
входит в базис, причем в строке для 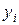 свободный член положителен, то исходная задача не имеет ни одного допустимого решения.
свободный член положителен, то исходная задача не имеет ни одного допустимого решения.
Составим симплекс-таблицы решаемой задачи.
| Базисные неизвест ные | Свободные члены | 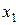
| 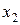
| 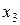
| 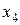
| 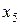
| 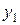
| 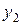
| 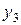
|
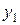
| –1 | ||||||||
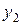
| –1 | ||||||||
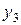
| 
| –1 | |||||||
| G | 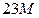
| 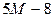
| 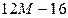
| 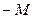
| 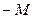
| 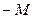
| |||
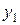
| 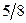
| –1 | 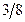
| 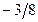
| |||||
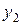
| 
| –1 | 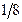
| 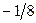
| |||||
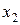
| 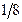
| 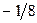
| 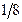
| ||||||
| G | 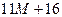
| 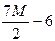
| 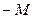
| 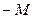
| 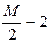
| 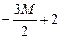
| |||
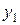
| 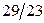
| –1 | 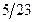
| 
| 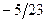
| 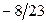
| |||
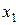
| 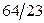
| 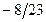
| 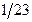
| 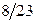
| 
| ||||
| 
| 
| 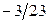
| 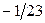
| 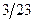
| ||||
| G | 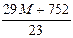
| 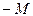
| 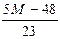
| 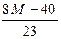
| 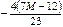
| 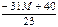
| |||
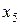
| 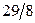
| 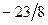
| 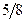
| 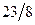
| 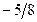
| –1 | |||
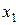
| 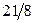
| 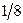
| 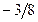
| 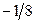
| 
| ||||
| 
| 
| 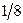
| 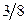
| 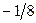
| ||||
| G | –5 | –1 | 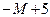
| 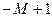
| 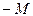
|
ЛЕКЦИЯ 6
Дата добавления: 2015-02-03; просмотров: 1236;
