Симплекс-метод для решения задач линейного программирования.
С увеличением числа неизвестных геометрический метод решения ЗЛП становится затруднительным при трех переменных и невозможным при большем числе переменных.
Поэтому был разработан универсальный метод решения ЗЛП – симплекс-метод, позволяющий решать ЗЛП в канонической форме.
Изложим суть симплекс-метода на примере задач с 5 неизвестными.
Пусть ЗЛП приведена к виду
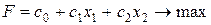 (20)
(20)
при ограничениях:
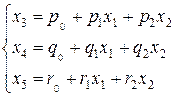 , (21)
, (21)
где 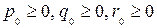 ,
,
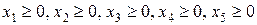 (22)
(22)
Про систему ограничений (21) говорят, что она имеет допустимый вид, если одни неизвестные ( 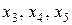 ) выражаются через остальные (
) выражаются через остальные ( 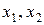 ), причем свободные члены этих выражений неотрицательны (
), причем свободные члены этих выражений неотрицательны ( 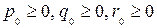 ).
).
Неизвестные 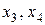 и
и 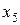 называются базисными, а неизвестные
называются базисными, а неизвестные 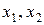 – свободными.
– свободными.
Возможны два принципиальных случая:
1Å Все коэффициенты при свободных неизвестных в выражении для F неположительны: 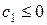 и
и 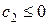 . Тогда для всякого неотрицательного решения системы уравнений (21) имеем
. Тогда для всякого неотрицательного решения системы уравнений (21) имеем 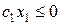 и
и 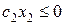 , а потому
, а потому
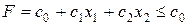 или
или 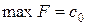 .
.
Следовательно, базисное решение 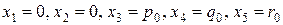 является оптимальными, т. е. задача решена.
является оптимальными, т. е. задача решена.
2Å Имеется свободное неизвестное, коэффициент при котором в выражении для F положителен, а все коэффициенты при этом неизвестном в уравнениях (21) – неотрицательны.
Для определенности положим 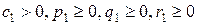 . Исходя из базисного решения, станем наращивать значение
. Исходя из базисного решения, станем наращивать значение  , не меняя
, не меняя 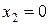 . Тогда значения базисных неизвестных будут оставаться неотрицательными:
. Тогда значения базисных неизвестных будут оставаться неотрицательными:
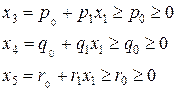 ,
,
а значение 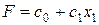 будет неограниченно возрастать, т.е.
будет неограниченно возрастать, т.е. 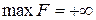 и задача решения не имеет.
и задача решения не имеет.
Решения ЗЛП редуцируются к одному из случаев 1Å или 2Å путем перехода к новому базису, в котором целевая функция не уменьшит своего значения для базисного решения, а новая система ограничений должна иметь допустимый вид. Преобразование базиса и перестройку целевой функции и системы ограничений называют шагом в решении ЗЛП. Таким образом, сделав нужное число шагов, решают ЗЛП (20) – (22).
Применим симплекс-метод к первой задаче.
I. Основная задача в примере 1 имеет вид
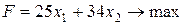
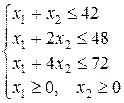
Сначала приведем ее к каноническому виду, вводя балансовые неизвестные 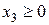 ,
, 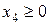 и
и 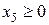 :
:
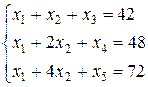 (23)
(23)
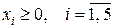 (24)
(24)
Теперь приведем (23) к допустимому виду – неизвестные 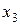 ,
, 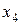 и
и 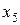 выразим через
выразим через  и
и 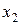 , при этом свободные члены в правых частях полученных уравнений неотрицательны:
, при этом свободные члены в правых частях полученных уравнений неотрицательны:
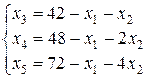 (25)
(25)
Здесь 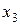 ,
, 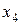 и
и 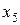 – базисные неизвестные, а
– базисные неизвестные, а  и
и 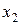 – свободные неизвестные.
– свободные неизвестные.
Шаг 1: положим в (25) 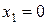 и
и 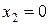 , тогда
, тогда 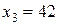 ,
, 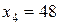 ,
, 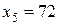 . Получим неотрицательное решение
. Получим неотрицательное решение 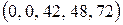 системы уравнений (25). Его называют базисным решением. Для него
системы уравнений (25). Его называют базисным решением. Для него 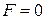 .
.
Шаг 2: положим в (25) 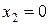 , а
, а  начнем наращивать так, чтобы
начнем наращивать так, чтобы 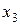 ,
, 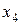 и
и 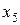 оставались неотрицательными, т. е.
оставались неотрицательными, т. е.
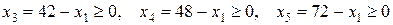 .
.
Решая эти неравенства, найдем наименьшее значение 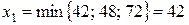 . Тогда
. Тогда 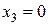 . Объявив
. Объявив 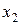 и
и 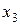 свободными неизвестными, приведем (25) к допустимому виду:
свободными неизвестными, приведем (25) к допустимому виду:
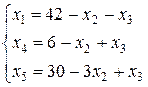 (26)
(26)
Получим неотрицательное решение 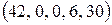 системы уравнений (26). Для него
системы уравнений (26). Для него
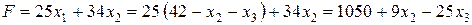 (27)
(27)
примет значение 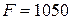 .
.
Сделаем выводы.
Во-первых, значение F по сравнению с 1-ым шагом увеличилось.
Во-вторых, в (27) коэффициент при 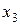 отрицательный и для дальнейшего увеличения значения F надо положить
отрицательный и для дальнейшего увеличения значения F надо положить 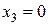 и наращивать
и наращивать 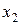 .
.
Шаг 3: положим в (26) 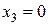 , а
, а 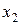 начнем наращивать так, чтобы
начнем наращивать так, чтобы  ,
, 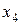 и
и 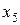 оставались неотрицательными, т. е.
оставались неотрицательными, т. е.
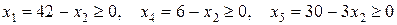 .
.
Откуда находим наименьшее значение 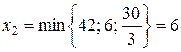 . Тогда
. Тогда 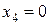 . Объявив
. Объявив 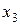 и
и 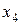 свободными неизвестными, приведем (27) к допустимому виду:
свободными неизвестными, приведем (27) к допустимому виду:
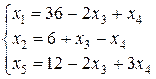 (28)
(28)
Получили неотрицательное решение 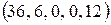 системы уравнений (28). Для него
системы уравнений (28). Для него
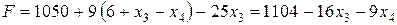 (29)
(29)
примет значение 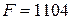 .
.
Сделаем выводы.
Во-первых, значение F по сравнению со 2-ым шагом увеличилось.
Во-вторых, в (29) оба коэффициента при свободных неизвестных отрицательны и дальнейшее увеличение значения F невозможно:
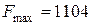
при 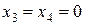 . Задача решена. Учитывая экономический смысл неизвестных, приходим к выводу: предприятие получит наибольшую прибыль 1104 единиц при изготовлении 36 единиц товара
. Задача решена. Учитывая экономический смысл неизвестных, приходим к выводу: предприятие получит наибольшую прибыль 1104 единиц при изготовлении 36 единиц товара 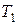 и 6 единиц товара
и 6 единиц товара 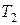 , при этом остатки ресурсов
, при этом остатки ресурсов 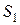 и
и 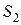 равны нулю (
равны нулю ( 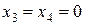 ), а остаток ресурса
), а остаток ресурса 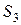 равен 12 единицам.
равен 12 единицам.
Если решается ЗЛП, в которой требуется найти минимум целевой функции, то задачу либо сводят к рассмотренной выше задаче с целевой функцией 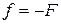 , либо с помощью шагов приводят к одному из двух принципиальных случаев:
, либо с помощью шагов приводят к одному из двух принципиальных случаев:
1Å Все коэффициенты при свободных неизвестных в выражении для F неотрицательны: 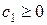 и
и 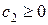 . Тогда базисное решение
. Тогда базисное решение 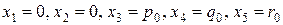 является решением задачи.
является решением задачи.
2Å Имеется свободное неизвестное, коэффициент при котором в выражении для F (20) отрицателен, а все коэффициенты при этом неизвестном в уравнениях (21) – неотрицательны. Тогда задача решения не имеет.
Применим симплекс-метод ко второй задаче, Основная задача в примере 2 имеет вид
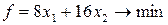
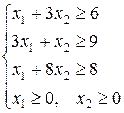
Сначала приведем ее к каноническому виду, вводя балансовые неизвестные 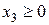 ,
, 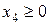 и
и 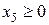 :
:
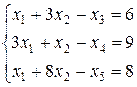 (30)
(30)
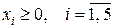 (31)
(31)
Приведем ограничения (30) к допустимому виду. Как показано выше, в качестве базисных неизвестных следует выбирать такие неизвестные, каждая из которых входит только в одно из уравнений системы ограничений (31), при этом нет таких уравнений системы, в которые не входит ни одна из этих неизвестных, и каждая базисная неизвестная имеет тот же знак, что и свободный член.
Нетрудно видеть, что 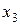 ,
, 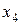 и
и 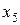 не могут быть базисными неизвестными. Действительно,
не могут быть базисными неизвестными. Действительно,
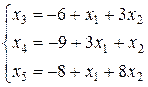 (32)
(32)
и знаки 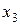 ,
, 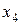 и
и 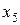 противоположны знакам свободных членов.
противоположны знакам свободных членов.
Для выделения базисных неизвестных из системы ограничений (30) необходима ее перестройка.
Полагая в (32) 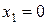 (или
(или 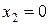 ) найдем из условий неотрицательности
) найдем из условий неотрицательности 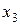 ,
, 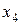 и
и 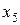 :
:
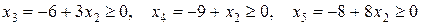 .
.
наибольшее значение 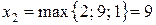 . Тогда
. Тогда 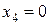 и систему (32) запишем в виде
и систему (32) запишем в виде
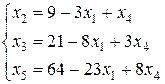 (33)
(33)
Получили систему ограничений, имеющую допустимый вид: 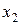 ,
, 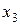 и
и 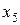 – базисные неизвестные,
– базисные неизвестные,  и
и 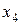 – свободные неизвестные. Перейдем к процедуре шагов.
– свободные неизвестные. Перейдем к процедуре шагов.
Шаг 1: положим в (33) 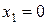 и
и 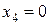 , тогда получим базисное решение
, тогда получим базисное решение 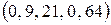 , для которого целевая функция
, для которого целевая функция
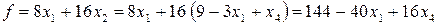 (34)
(34)
примет значение 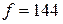 .
.
В (5.15) коэффициент при 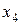 положительный и для дальнейшего уменьшения значения f надо положить
положительный и для дальнейшего уменьшения значения f надо положить 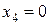 и наращивать
и наращивать  .
.
Шаг 2: положим в (33) 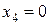 , а
, а  начнем наращивать так, чтобы
начнем наращивать так, чтобы 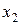 ,
, 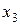 и
и 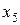 оставались неотрицательными, т. е.
оставались неотрицательными, т. е.
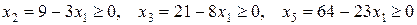 .
.
Откуда находим 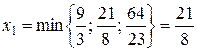 . Тогда
. Тогда 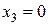 . Объявив
. Объявив 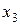 и
и 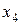 свободными неизвестными, приведем (33) к допустимому виду:
свободными неизвестными, приведем (33) к допустимому виду:
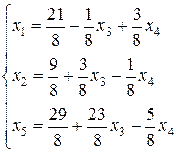 (35)
(35)
Из (35) получим базисное решение 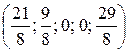 . Для него
. Для него
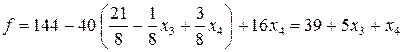 (36)
(36)
примет значение 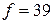 .
.
В (36) коэффициенты при свободных неизвестных положительны и дальнейшее уменьшение значения f невозможно: 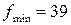 при
при 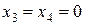 . Задача решена.
. Задача решена.
Учитывая экономический смысл неизвестных, приходим к выводу.
Ежесуточная диета, обеспечивающая необходимое количество питательных веществ, состоит из 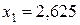 единиц продукта
единиц продукта 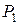 ,
, 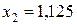 единиц продукта
единиц продукта 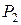 и ее минимальная стоимость
и ее минимальная стоимость 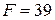 единиц. При этом потребности организма в питательных веществах A и B отвечают требуемым минимальным объемам
единиц. При этом потребности организма в питательных веществах A и B отвечают требуемым минимальным объемам 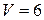 единиц и
единиц и 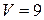 единиц соответственно (т.к.
единиц соответственно (т.к. 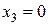 и
и 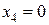 ), а потребности в питательном веществе С больше требуемого минимального объема
), а потребности в питательном веществе С больше требуемого минимального объема 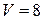 единиц на
единиц на 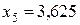 единиц.
единиц.
В заключение рассмотрим вопрос: всегда ли после конечного числа шагов симплекс-метод закончится либо нахождением оптимального решения, либо установлением того факта, что задача не имеет решения.
Ответ утвердительный и содержится в следующей теореме.
Теорема. Если существует оптимальное решение ЗЛП, то существует и базисное оптимальное решение. Последнее всегда может быть получено с помощью симплекс-метода.
Дата добавления: 2015-02-03; просмотров: 1264;
