Продуктивные модели.
В экономике существует баланс между отдельными отраслями. Рассмотрим простой вариант модели межотраслевого баланса – модель «затраты-выпуск».
Пусть имеется n различных отраслей, каждая из которых производит свой продукт и нуждается в продукции других отраслей (производственное потребление). Введем следующие обозначения:
xi ‑ общий объем продукции отрасли i за плановый год ‑ так называемый валовой выпуск отрасли i;
xij ‑ объем продукции отрасли i, расходуемый отраслью j в процессе производства;
yi ‑ объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере ‑ объем конечного потребления. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.
Указанные величины сведем в таблицу.
| Производственное потребление | Конечное Потребление | Валовой выпуск |
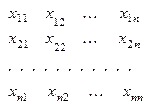
| 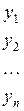
| 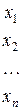
|
Балансовый характер этой таблицы выражается в том, что при любом 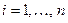 выполняется соотношение
выполняется соотношение
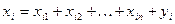 , (1)
, (1)
означающее, что валовойвыпуск xi расходуется на производственное потребление, равное 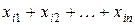 , и непроизводственное потребление, равное уi. Соотношения (1) называют соотношениями баланса.
, и непроизводственное потребление, равное уi. Соотношения (1) называют соотношениями баланса.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т. п.), или стоимостными. В зависимости от этого различают натуральныйи стоимостной межотраслевой балансы. В дальнейшем будем иметь в виду стоимостной баланс.
В. Леонтьев обратил внимание на важное обстоятельство: величины  остаются постоянными в течение ряда лет, что объясняется примерным постоянством используемой технологии производства.
остаются постоянными в течение ряда лет, что объясняется примерным постоянством используемой технологии производства.
Сделаем следующее допущение: для выпуска любого объема xj продукции отрасли j необходимо затратить продукцию отрасли i в количестве 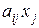 , т.е. материальные издержки пропорциональны объему производимой продукции:
, т.е. материальные издержки пропорциональны объему производимой продукции:
 . (2)
. (2)
Коэффициенты 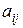 называют коэффициентами прямых материальных затрат или коэффициентами материалоемкости. Они показывают сколько необходимо единиц продукции отрасли i для производства единицы продукции отрасли j, если учитывать только прямые затраты.
называют коэффициентами прямых материальных затрат или коэффициентами материалоемкости. Они показывают сколько необходимо единиц продукции отрасли i для производства единицы продукции отрасли j, если учитывать только прямые затраты.
Подставив (2) в балансовое соотношения (1), получим

или, в матричной записи,
 , (3)
, (3)
где
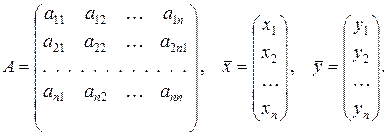
Вектор 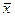 называется вектором валового выпуска, вектор
называется вектором валового выпуска, вектор  ‑ вектором конечного потребления, а матрица А ‑ матрицей прямых затрат. Соотношение (3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов
‑ вектором конечного потребления, а матрица А ‑ матрицей прямых затрат. Соотношение (3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов 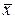 и
и  это соотношение называют также моделью Леонтьева.
это соотношение называют также моделью Леонтьева.
Уравнения межотраслевого баланса можно использовать для плановых расчетов:
- задавая для каждой отрасли i валовой выпуск продукции 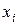 можно определить объемы конечного потребления каждой отрасли
можно определить объемы конечного потребления каждой отрасли 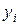 :
:
 ,
,
где Е – единичная матрица;
- задавая величины конечного потребления каждой отрасли 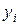 можно определить величины валового выпуска продукции
можно определить величины валового выпуска продукции 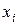 :
:
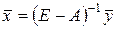 ,
,
где 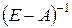 – матрица, обратная к матрице
– матрица, обратная к матрице  , ее элементы называют коэффициентами полных материальных затрат.
, ее элементы называют коэффициентами полных материальных затрат.
Отметим особенности системы (3): все компоненты матрицы А, а также векторов 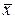 и
и  неотрицательны (это вытекает из экономического смысла А,
неотрицательны (это вытекает из экономического смысла А, 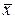 и
и  ). Для краткости будем записывать это так:
). Для краткости будем записывать это так: 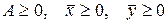 .
.
Таким образом, плановые расчеты по модели Леонтьева можно выполнять при соблюдении следующего условия продуктивности:
матрица 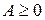 называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора 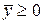 существует решение
существует решение 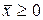 уравнения (3).
уравнения (3).
В этом случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.
Сформулируем критерии продуктивности матрицы 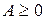 .
.
Критерий I. Матрица 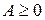 продуктивна тогда и только тогда, когда матрица
продуктивна тогда и только тогда, когда матрица 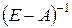 существует и неотрицательна.
существует и неотрицательна.
Критерий II. Матрица 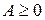 продуктивна тогда и только тогда, когда имеет место разложение матрицы
продуктивна тогда и только тогда, когда имеет место разложение матрицы 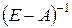 в матричный ряд
в матричный ряд
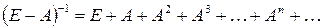 . (4)
. (4)
В соотношении (4) матрицы  называются матрицами коэффициентов косвенных затрат 2-го, 3-го и т.д. порядков. Их сумма образует матрицу коэффициентов косвенных затрат
называются матрицами коэффициентов косвенных затрат 2-го, 3-го и т.д. порядков. Их сумма образует матрицу коэффициентов косвенных затрат
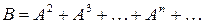 . (5)
. (5)
Суть косвенных затрат поясним на примере производства двигателей. На их изготовление в виде прямых затрат расходуется сталь, чугун и т.д. Но для производства стали также нужен чугун. Следовательно, производство двигателей включает как прямые, так и косвенные затраты чугуна.
Таким образом, из соотношений (4) и (5) имеем
 , (6)
, (6)
т.е. матрица коэффициентов полных материальных затрат включает в себя матрицы коэффициентов прямых и косвенных затрат.
Рассмотрим примеры.
Пример 1. Исследовать на продуктивность матрицу

Решение. Сначала найдем матрицу 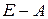 :
:

Затем найдем 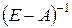 . С этой целью по известным из линейной алгебры правилам вычислим определитель
. С этой целью по известным из линейной алгебры правилам вычислим определитель

алгебраические дополнения для элементов матрицы 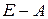
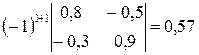 ;
;  ;
;
 ;
; 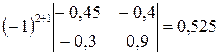 ;
;
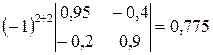 ;
;  ;
;
 ;
; 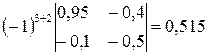 ;
;
 .
.
Тогда
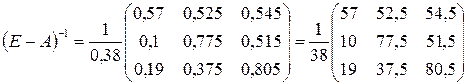
Полученная матрица неотрицательна и по Критерию I исходная матрица А продуктивная.
Пример 2. Для матрицы А коэффициентов прямых затрат из примера 1 и вектора конечного потребления

найти: а) вектор валового выпуска; б) матрицу косвенных затрат; в) изменение вектора валового выпуска при увеличении вектора конечного потребления на величину
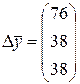
Решение.
а) Вектор валового выпуска 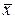 вычислим по формуле
вычислим по формуле
 .
.
Имеем
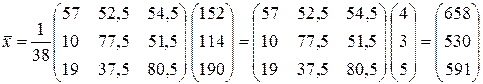
б) Матрицу косвенных затрат В найдем из соотношения (2.6):
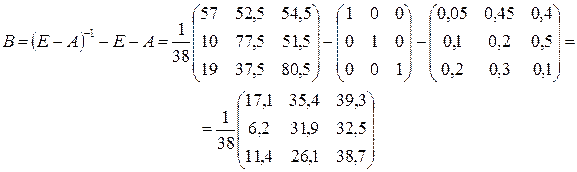
в) 
Таким образом, при увеличении вектора конечного потребления на 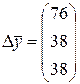 вектор валового выпуска увеличится на
вектор валового выпуска увеличится на  .
.
ЛЕКЦИЯ 3,4,5
Дата добавления: 2015-02-03; просмотров: 1475;
