Диффузионные модели.

В основе диффузионной модели лежит допущение, что структура потока описывается уравнением, аналогичным уравнению молекулярной диффузии. Параметром модели является коэффициент продольного перемешивания, называемый также коэффициентом турбулентной диффузии (или коэффициентом обратного перемешивания).

Для вывода уравнения модели составим уравнение материального баланса для элемента аппарата Δx, как показано на рис. 1. Приняты следующие обозначения: F - сечение аппарата, м²; и - скорость потока, м/с; t — время, с; С — концентрация индикатора, кг/м³; D_l — коэффициент продольного перемешивания, м² /с.

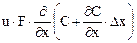В рассматриваемый элемент поступают конвективный поток u F C и поток, вызываемый турбулентной диффузией ,а покидают рассматриваемый элемент конвективный поток и поток, вызываемый турбулентной диффузией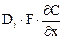

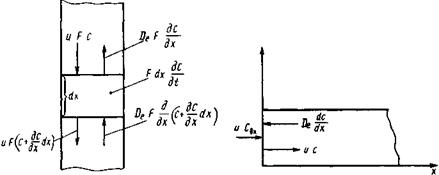
Рис. 1. К выводу уравнения диффузной ной модели

Рис. 2. Схема потоков у левого конца аппарата

В соответствии с законом сохранения массы разность между входящими и выходящими потоками должна составлять накопление вещества (индикатора) в рассматриваемом элементе. Она равна 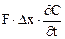. Запишем теперь уравнение сохранения массы:

Накопление = Приход вещества - Расход вещества

или

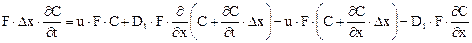
Преобразуя последнее уравнение и переходя к пределу при Δх → 0, получаем

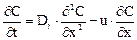
Уравнение является основным уравнением диффузионной модели.

Остановимся на начальном и граничном условиях для уравнения. Очевидно, что должны быть заданы одно начальное и два граничных условия. В качестве начального условия обычно задается профиль концентраций по аппарату в начальный момент времени:

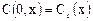при t=0.

Граничные условия могут быть заданы из условия материального баланса на концах аппарата (условия по Данквертсу). Рассмотрим левый конец аппарата, в который поступает поток с некоторой средней скоростью и (рис. 2).

Рис. 3. Схема потоков у правого конца аппарата

Сумма потоков вещества, подходящих к границе х = 0, должна быть равна потоку вещества, отходящего от границы. Тогда получим

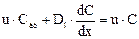
или

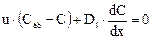
Для правого конца аппарата (рис. 3) имеем

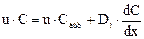
На практике часто принимают С = С_ВЫХ. Сучетом этого граничное условие примет вид

Условия в таком виде называются граничными условиями по Данквертсу.