Передаточная функция диффузионной модели при импульсном возмущении.
Как известно передаточная функция при импульсном возмущении равна изображению выходного сигнала.
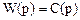
Запишем уравнение диффузионной модели в безразмерной форме использую преобразование по Лапласу.
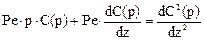
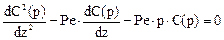
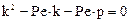
Решение примет вид:
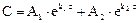 , где А1 и А2 константы интегрирования.
, где А1 и А2 константы интегрирования.
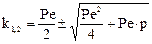 ;
; 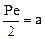 ;
; 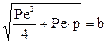
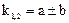
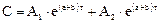
А1 и А2 определяем из граничных условий.
При импульсном возмущении изображение входного сигнала 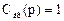 ; граничные условия примут вид:
; граничные условия примут вид:
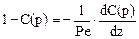
Продифференцируем решение уравнения по z и найдем:
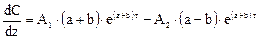
и подставим в граничное условие откуда выразим А1 или А2:
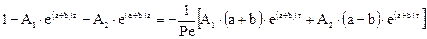
Из последнего уравнения выражают одну из констант, а из другого граничного условия выражают вторую константу и подставляют в исходное уравнение вместо А1 и А2 получают передаточную функцию объекта описываемого диффузинонной моделью.
Как видно из уравнений передаточная функция содержит параметр Ре в котором неизвестным является коэффициент продольного перемешивания DL, который определяется по экспериментальной С-кривой.
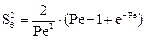
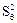 - безразмерная дисперсия равная
- безразмерная дисперсия равная 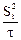 , выразим ее через
, выразим ее через 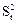 - размерную дисперсию:
- размерную дисперсию:
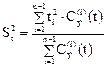
Определяем τ через С – кривую.
Если Ре > 10, то 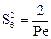
Дата добавления: 2015-03-03; просмотров: 1042;
