Ячеечная модель.

Вывод основных уравнений модели. Рассматриваемая модель, впервые предложенная для каскада реакторов с мешалками, является одной из наиболее простых. В этом случае аппарат состоит из ряда последовательно соединенных ячеек, через которые проходит поток вещества (рис. 1).

Сделаем следующие допущения: 1) в каждой ячейке осуществляется идеальное перемешивание; 2) между ячейками отсутствует обратное перемешивание. Параметром ячеечной модели, количественно характеризующим продольное перемешивание, служит число ячеек полного перемешивания N. С увеличением N структура потока приближается к модели полного вытеснения, а с уменьшением N— кмодели идеального смешения.

Запишем уравнения сохранения массы для каждой из ячеек (для простоты предположим, что ячейки имеют одинаковый объем V_я) :

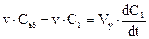
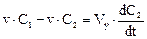
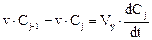
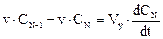
Рис. 1. Схема ячеечной модели: υ - расход вещества через аппарат; С_вх - концентрация на входе

Разделив левую и правую части уравнений на расход υ, получаем:

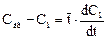
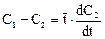
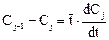
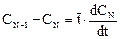
Соответствующие начальные условия для системы уравнений имеют вид

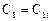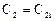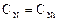, , ..., при t =0.

Система уравнений вместе с начальными условиями образуют ячеечную модель структуры потоков. Для того чтобы проанализировать свойства модели, рассмотрим отклики ячеечной модели на стандартные возмущения.