Передаточная функция объектов, описываемых ячеечной моделью.

Согласно определению передаточная функция объекта W(p) имеет вид

,

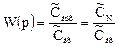Умножим и разделим правую часть равенства на С_N-1.

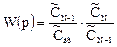
Второй сомножитель в правой части уравнения представляет собой передаточную функцию Ν-ойячейки, т.е. W_N(p). Тогда последнее уравнение можно переписать в виде

Аналогично, умножив и разделив правую часть равенства на C_N-2, получим

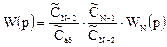
Второй сомножитель в правой части уравнения является передаточной функцией (N— 1) -и ячейки. Тогда уравнение можно записать в виде

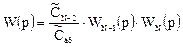
Проводя аналогичные преобразования, приходим к следующему выражению для передаточной функции объекта, описываемого ячеечной моделью:

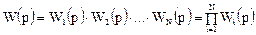
Так как в ячеечной модели каждая ячейка представляется моделью идеального смешения, то

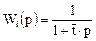
где — среднее время пребывания в ячейке (предполагается, что ячейки имеют равный объем).

С учетом выражения получаем окончательное выражение для передаточной функции ячеечной модели:

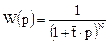
Рассмотрим теперь следующие предельные случаи.

1. Число ячеек N в ячеечной модели равно 1. В этом случае передаточная функция имеет вид

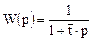
Выражение соответствует передаточной функции модели идеального смешения и ячеечная модель соответственно переходит в модель идеального смешения.

2. Число ячеек N в ячеечной модели стремится к бесконечности. В этом случае имеем

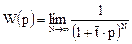
Пусть 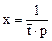и 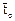- среднее время пребывания в объекте, описываемом ячеечной моделью. Тогда

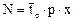
Подставляя в уравнение, имеем

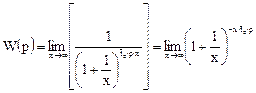
или

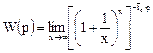
Учитывая, что

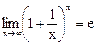
получаем следующее выражение для передаточной функции:

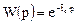
Передаточная функция соответствует модели идеального вытеснения. Следовательно, в случае, когда N→∞, ячеечная модель переходит в модель идеального вытеснения.