Функция отклика ячеечной модели на импульсное возмущение.
Для получения функции отклика ячеечной модели будем аналогично предыдущему случаю находить отклики на выходе первой, второй и т.д. ячеек.
Первая ячейка.
Так как концентрация на входе Свх в первую ячейку для импульсного возмущения равна нулю, то уравнение сохранения вещества примет вид
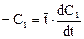
Его решение есть
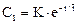
Неизвестную константу К находим из начального условия
С1 = Сн при t = 0.
Отсюда
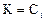 и
и
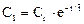
Вторая ячейка.
Входом во вторую ячейку является выход из первой. Тогда для второй ячейки имеем
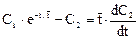
Решаем сначала соответствующее однородное уравнение
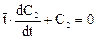 , которое после разделения переменных примет вид
, которое после разделения переменных примет вид
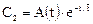
Для нахождения неизвестного множителя A(t)подставим решение в исходное уравнение:
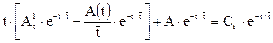
После приведения подобных членов в уравнении приходим к дифференциальному уравнению первого порядка относительно A(t):
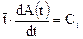
Его решение есть
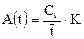
Подставляя в уравнение и учитывая начальное условие C1·=0 при t = 0, получаем функцию отклика на выходе второй ячейки:
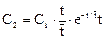
Аналогичные решения для третьей, четвертой, ..., ν-1 ячейки дают следующую общую функцию отклика ячеечной модели, включающей N ячеек:
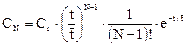
Дата добавления: 2015-03-03; просмотров: 1128;
