Определение параметров ячеечной модели.
Оценка параметра N ячеечной модели. Для оценки параметра N ячеечной модели определим начальный момент второго порядка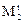 
. для функции отклика на импульсное возмущение, воспользовавшись передаточной функцией этой модели. Имеем
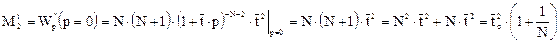
Соответственно центральный размерный момент второго порядка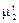 
определяется выражением
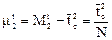
Разделив выражение на квадрат среднего времени пребывания в системе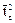 
, получаем уравнение связи параметра ячеечной модели N с безразмерной дисперсией 
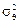функции отклика ячеечной модели на импульсное возмущение:
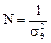
Выражение - основное для оценки параметра ячеечной модели Ν по экспериментальным кривым отклика на импульсное возмущение.
Сравнивая выражения для диффузионной модели и ячеечной, получаем следующее уравнение связи между параметрами диффузионной и ячеечной моделей:
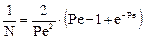
При Ре > 10 последнее соотношение можно упростить. В этом случае уравнение связи принимает вид
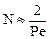
Ориентировочные области применения различных моделей структуры потоков в аппарате
| Наименование модели | Области применения |
| Модель идеального вытеснения | Трубчатые аппараты с отношением длины к диаметру свыше 20 |
| Модель идеального перемешивания | Цилиндрические аппараты со сферическим дном в условиях интенсивного перемешивания с отражательными перегородками; барботажные аппараты с близкими размерами диаметра и высоты в условиях интенсивного барботажа |
| Ячеечная модель | Каскады реакторов с мешалками; тарельчатые колонны; аппараты с псевдоожиженными слоями; насадочные колонны |
| Рециркуляционная модель | Тарельчатые, секционированные насадочные аппараты, где наблюдается заброс вещества в сторону, противоположную направлению основного потока (например, пульсационные колонные аппараты) |
| Диффузионная модель | Трубчатые аппараты; аппараты колонного типа с насадкой и без насадки при осевом рассеивании вещества |
Дата добавления: 2015-03-03; просмотров: 1195;