Комбинированные модели, составленные из параллельно соединенных зон.
Рассмотрим в качестве примера параллельное соединение зон идеального смешения и идеального вытеснения (рис. 11).
Из условия материального баланса в точке Z получаем
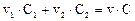
Поэтому концентрация на выходе составляет
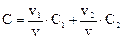
Определим отклик системы на импульсное и ступенчатое возмущения. Из уравнения следует, что такой отклик является суммой откликов модели идеального смешения и идеального вытеснения с коэффициентами υ1/υ и υ2/υ. На рис. 9 и 10 изображены кривые отклика на стандартные возмущения системы, состоящей из параллельного соединения зон идеального смешения и идеального вытеснения.
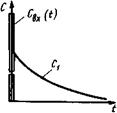
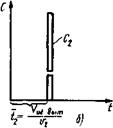
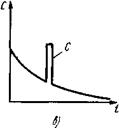
Рис. 9. Отклик системы, составленной из параллельно соединенных зон идеального смешения и идеального вытеснения на импульсное возмущение: а - отклик зоны идеального смешения; б - отклик зоны идеального вытеснения; в - отклик системы
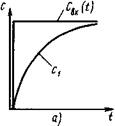
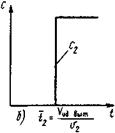
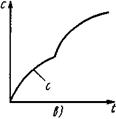
Рис. 10. Отклик системы, составленной из параллельно соединенных зон идеального смешения и идеального вытеснения на ступенчатое возмущение: а - отклик зоны идеального смешения; б - отклик зоны идеального вытеснения; в - отклик системы
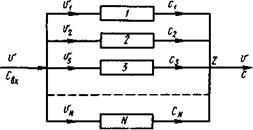
Рис. 11. Структура потоков в системе из параллельно соединенных зон
Найдем передаточную функцию системы, составленной из параллельно соединенных зон. Пусть рассматриваемая система состоит из N зон, параллельно соединенных между собой (рис. 11).
Запишем уравнение материального баланса для узла Z:
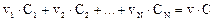
откуда, обозначая ki = υi·/υ, получаем
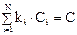
Применим к уравнению преобразование Лапласа и разделим полученное уравнение на преобразованную по Лапласу входную концентрацию 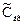 . Имеем
. Имеем
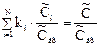
Отношения 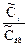 в левой части уравнения представляют собой передаточные функции Wi(p) соответствующих зон, а отношение
в левой части уравнения представляют собой передаточные функции Wi(p) соответствующих зон, а отношение 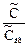 - передаточную функцию всей системы в целом, т.е. Wc(p). Тогда получаем следующее соотношение между передаточной функцией системы и передаточными функциями отдельных зон:
- передаточную функцию всей системы в целом, т.е. Wc(p). Тогда получаем следующее соотношение между передаточной функцией системы и передаточными функциями отдельных зон:
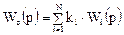
Найдем среднее время пребывания в системе, составленной из параллельно соединенных зон. Используя выражение для передаточной функции системы, имеем
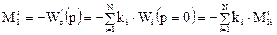
где 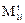 - первые начальные моменты отдельных зон системы.
- первые начальные моменты отдельных зон системы.
Так как . 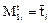 (
( 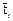 - среднее время пребывания в i-й зоне) и
- среднее время пребывания в i-й зоне) и 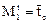 , то
, то 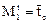
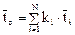
Определим дисперсию функции отклика системы, составленной из параллельно соединенных зон. Сначала найдем второй начальный момент функции отклика:
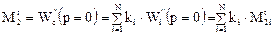
где 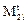 - вторые начальные моменты функций отклика отдельных зон. Используя теперь связь безразмерной дисперсии со вторым начальным моментом, выражаемую равенством
- вторые начальные моменты функций отклика отдельных зон. Используя теперь связь безразмерной дисперсии со вторым начальным моментом, выражаемую равенством
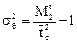
получаем
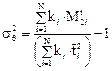
Дата добавления: 2015-03-03; просмотров: 1008;
