Комбинированные модели, составленные из последовательно соединенных зон.

Рис. 12. Последовательное соединение зон.
Рассмотрим передаточную функцию системы, составленной из последовательно соединенных зон. Пусть система включает несколько зон, последовательно соединенных между собой. Тогда в соответствии с определением передаточной функции Wc можно записать
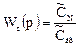
где 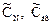 — соответственно выходная и входная концентрации, преобразованные по Лапласу.
— соответственно выходная и входная концентрации, преобразованные по Лапласу.
Умножив и разделив правую часть последнего равенства на 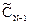 , получаем
, получаем
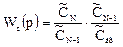
Аналогично, умножив и разделив правую часть уравнения на 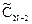 ,
, 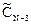 ,
, 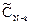 приходим к следующему уравнению:
приходим к следующему уравнению:
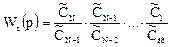
Сомножители 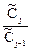 (j =1,2 … N) представляют собой не что иное,
(j =1,2 … N) представляют собой не что иное,
как передаточные функции отдельных зон. Тогда уравнение можно записать в виде
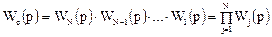
Итак, согласно полученному соотношению, передаточная функция системы Wc(p) из последовательно соединенных зон равна произведению передаточных функций Wj(p) отдельных зон.
Определим среднее время пребывания 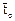 в системе, составленной из последовательно соединенных зон. Для этого воспользуемся передаточной функцией системы Wc(p). Пусть N = 2. Тогда
в системе, составленной из последовательно соединенных зон. Для этого воспользуемся передаточной функцией системы Wc(p). Пусть N = 2. Тогда
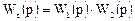
и первый начальный момент системы есть
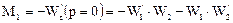
Так как при р= 0 Wl = М1 = 1 и W1’ = Μ1; W2' = -М2 (здесь М1 и М2 - первые начальные моменты первой и второй зон соответственно), то
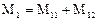
Рассматривая аналогично случаи Ν— 3, 4,..., получаем следующую формулу для среднего времени пребывания в системе:
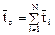
Найдем теперь дисперсию функции отклика системы, составленной из последовательно соединенных зон. Аналогично предыдущему будем использовать передаточную функцию системы. Рассмотрим случай N = 2. Тогда второй начальный момент есть
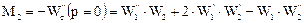
Так как W1(p=0)=l, a W2(p = 0) = -Μ2, то
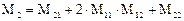
Отсюда находим дисперсию функции отклика системы:
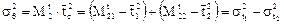
где 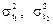 — дисперсии функции отклика составляющих зон.
— дисперсии функции отклика составляющих зон.
Аналогично рассматривая случаи N = 3, 4, ..., получаем следующее соотношение для дисперсии функции отклика системы из N зон:
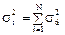
Соответственно безразмерная дисперсия есть
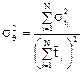
Дата добавления: 2015-03-03; просмотров: 985;
