Рецикл.
Рассмотрим явление рециркуляции потока с выхода на вход аппарата (рис. 6).
Найдем выражение для передаточной функции в данной системе. Уравнение материального баланса для узла S запишется в виде
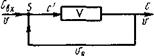
Рис. 6. Структура потоков в аппарате с рециркуляцией.
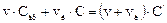
Применив к уравнению преобразование Лапласа, имеем
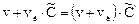
где 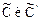 — преобразованные по Лапласу концентрации.
— преобразованные по Лапласу концентрации.
Обозначим отношение рециркуляционного потока υк к основному υ через R. Тогда, разделив последнее уравнение на υ С, получаем следующее уравнение:
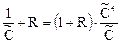
Отношение 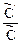 представляет собой передаточную функцию аппарата без учета рецикла. Будем считать, что передаточная функция аппарата без рецикла W(p) соответствует модели идеального смешения, т.е.
представляет собой передаточную функцию аппарата без учета рецикла. Будем считать, что передаточная функция аппарата без рецикла W(p) соответствует модели идеального смешения, т.е.
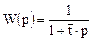
где  — среднее время пребывания без учета рецикла. Теперь уравнение перепишется так:
— среднее время пребывания без учета рецикла. Теперь уравнение перепишется так:
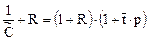 или
или 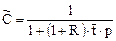
Для импульсного возмущения на входе передаточная функция аппарата с рециклом W (р) равна С. Следовательно,
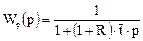
Найдем среднее время пребывания и дисперсию функции отклика аппарата с рециклом, используя передаточную функцию. Первый начальный момент нормированной С-кривой есть
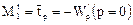
После дифференцирования выражения получаем
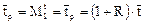
Таким образом, среднее время пребывания в аппарате с рециклом в 1 + R раз больше среднего времени пребывания в отсутствие рецикла.
Выразим второй начальный момент через передаточную функцию:
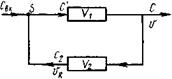
Рис 7. Схема потоков в аппарате с рециркуляцией потока через объем
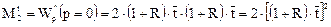
Отсюда находим дисперсию
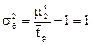
Рассмотрим теперь случай, когда рециркуляционный поток с выхода аппарата возвращается на вход через определенный объем V2 (рис. 7) Запишем уравнение материального баланса для узла:
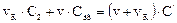
Применим преобразование Лапласа к уравнению, считая, что концентрация на входе Cвх соответствует импульсному возмущению. Имеем
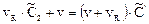
откуда, разделив на 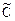 , получаем
, получаем
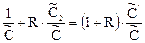
где
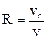
Отношение преобразованных по Лапласу концентраций 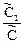 представляет собой передаточную функцию W2(p) объема V2, а отношение
представляет собой передаточную функцию W2(p) объема V2, а отношение 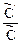 — передаточную функцию W1(p) объема V1. Таким образом,
— передаточную функцию W1(p) объема V1. Таким образом,
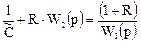
Разрешая последнее уравнение относительно С, находим
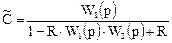
Дата добавления: 2015-03-03; просмотров: 1609;
