Отклики модели на ступенчатое возмущение.

Определим концентрацию на выходе каждой из ячеек.

Первая ячейка.

Так как для данного вида возмущения концентрация на входе С_вх отлична от нуля, то уравнение сохранения вещества для первой ячейки запишется следующим образом:

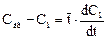, а начальное условие имеет вид

С₁ = 0 при t = 0.

Уравнение можно представить в виде

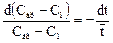
Интегрирование последнего уравнения дает

Константу интегрирования К найдем из начального условия

К = С_вх при t = 0.

Тогда на выходе первой ячейки получим следующую функцию отклика:

Вторая ячейка.

Входом для второй ячейки является отклик первой ячейки. В этом случае уравнение сохранения вещества для второй ячейки запишется так:

Решение соответствующего однородного уравнения есть

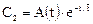
Для отыскания неопределенного множителя A(t) подставим решение в исходное неоднородное уравнение:

Приводя подобные члены, получаем следующее уравнение относительно искомого множителя A(t):

Его решение есть

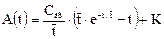
Подставляя теперь выражение в уравнение, получаем решение неоднородного дифференциального уравнения:

Константу К найдем из начального условия С₂ =0,.К = -С_вх при t = 0.

Подстановка в уравнение дает отклик на выходе второй ячейки:

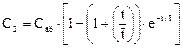
Продолжая аналогичные рассуждения для третьей, четвертой, N-1 ячейки, получаем следующую функцию отклика на выходе из последней N-й ячейки:

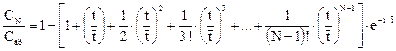
На рис. 3 изображена зависимость выходной концентрации при ступенчатом возмущении для различного числа ячеек.

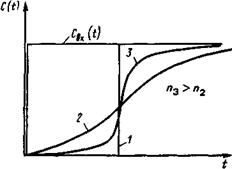
Рис. 3. Отклик ячеечной модели на ступенчатое возмущение: 1 — при идеальном вытеснении; 2, 3 - при числе ячеек n₂ и n₃ соответственно