Волновая функция

Возникает вопрос, как математически описать такое поведение электрона, чтобы можно было теоретически получить ту интерференционную картину, которую мы видим на эксперименте. Это можно сделать с помощью аппарата волновых функций. Согласно основным положениям квантовой механики, состояние любой системы можно описать некоторой функцией (которая называется волновой функцией). Эту функцию принято обозначать буквой греческого алфавита «пси». Например, волновую функцию электрона запишем как
Y(r₀, t₀; r, t). Эта волновая функция описывает перемещение электрона из точки r₀, в которой он находился в момент времени t₀, в точку r в момент времени t. В общем случае эта функция является комплексной величиной. Квадрат ее модуля |Y(r₀, t₀; r, t)|² = Y*(r₀, t₀; r, t)Y(r₀, t₀; r, t) определяет вероятность того, что электрон, находившийся в момент t₀ в точке r₀, в момент времени t окажется в точке r. Волновая функция находится из решения уравнения Шредингера. Причем решение этого уравнения, т. е. конкретный вид волновой функции, зависит от граничных условий. В применении к нашей задаче это означает, что электрон, вылетевший в момент t₀ из источника в точке r₀, прошедший через щель 1 и попавший в детектор, расположенный в точке r_D, будет описываться волновой функцией Y₁(r₀, t₀; r_D, t). Аналогично электрон, вылетевший в момент t₀ из источника в точке r₀, прошедший через щель 2 и попавший в детектор, расположенный в точке r_D, будет описываться волновой функцией Y₂(r₀, t₀; r_D, t).

Только что сказанное вовсе не означает, что электрон на самом деле проходит через щель 1 или щель 2. Это просто возможные сценарии или, если хотите, возможные траектории движения электрона. Обе эти возможности являются независимыми друг от друга, т. е. попадание электрона в детектор может произойти двумя независимыми способами. В этом случае, согласно правилам квантовой механики, волновая функция, описывающая перемещение электрона из точки r₀ в момент t₀ в точку r_D в момент t, будет суммой двух волновых функций:

Y(r₀, t₀; r_D, t) = Y₁(r₀, t₀; r_D, t) + Y₂(r₀, t₀; r_D, t).

Вероятность того, что электрон, вылетевший из точки r₀ в момент t₀, попадет в точку r_D в момент t, будет равна квадрату модуля этой волновой функции:

|Y(r₀, t₀; r_D, t)|² = |Y₁(r₀, t₀; r_D, t) + Y₂(r₀, t₀; r_D, t)|² =

= (Y₁ + Y₂)(Y₁^* + Y₂^*) = |Y₁|² + |Y₂|² + Y₁Y₂^* + Y₁^*Y₂ .

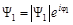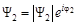Поскольку волновые функции являются в общем случае комплексными, их можно записать в виде и . Тогда получим

.

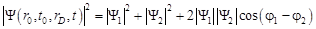Последнее слагаемое в этой формуле как раз и приводит к интерференционному эффекту. Разность фаз j₁ - j₂ зависит от положения детектора и при его перемещении меняется от 0 до 2p. При этом cos(j₁ - j₂) меняется от +1 до -1, давая усиление или ослабление вероятности.

Подчеркнем еще раз, что такой подход не позволяет предсказать исход единичного эксперимента. Можно только предсказать количество заданных исходов, проведя много тождественных экспериментов. То есть мы не можем, даже зная волновую функцию, предсказать, попадет ли в детектор, находящийся в точке r_D, конкретный электрон, вылетевший из источника в момент t₀. Но мы можем, зная волновую функцию, предсказать, что, скажем, из 100 электронов в детектор попадет примерно 25 электронов. Если же эксперимент ставится так, что каждый раз определяют, какая из альтернативных возможностей осуществляется (т. е. мы экспериментально определяем, через какую щель пролетел электрон), то надо складывать вероятности

.

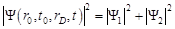В этом случае никакой интерференционной картины не получается.

5. Интерференция с одиночными электронами.
Эксперимент

Любопытно, что в 3-м томе своих лекций Фейнман, теоретически описывая эксперимент с электронами, который мы только что рассмотрели, пишет: «не пытайтесь проделать этот опыт. Этот опыт никто никогда так не ставил. Все дело в том, что для получения интересующих нас эффектов прибор должен быть чересчур миниатюрным. Мы с вами ставим сейчас мысленный эксперимент, отличающийся от других тем, что его легко обдумать». Вероятно, Фейнман не знал, что первый эксперимент такого рода с электронами был выполнен в том же 1961 г., когда он начал читать свои лекции (которые были изданы в 1963 г.). Фейнман также нигде не говорит о том, что такая же интерференционная картина получится, если выпускать электроны один за одним подобно описанному выше эксперименту с дифракцией одиночными электронами.

Как бы там ни было, первый интерференционный эксперимент с рассеянием электронов на двух щелях был выполнен в Германии в 1961 г. Клаусом Йонссоном в университете г. Тюбингена. Эта работа осталась практически незамеченной, вероятно, потому, что была опубликована в немецком научном журнале. Эксперимент же с одиночными электронами впервые осуществлен группой итальянских физиков в 1974 г. в Болонском университете и спустя 15 лет повторен в 1989 г. на более чувствительной аппаратуре японскими учеными из фирмы Hitachi (A. Tonomura и др.).

В этом эксперименте, схема которого показана на рис. 6.10^*, источником электронов служил электронный микроскоп. Электроны, вылетавшие из микроскопа, имели скорость примерно 40 % от скорости света (120 000 км/с). С такой скоростью электрон может за секунду три раза обогнуть Землю. Расстояние от источника до детектора, равное примерно одному метру, электрон пролетал за одну стомиллионную долю секунды. За одну секунду источник испускал всего 10 электронов. Это значит, что в момент регистрации электрона детектором следующий электрон еще не вылетел из источника! Поэтому в каждый момент времени в установке между источником и детектором находился только один электрон. Электроны проходили через устройство – так называемую электронную бипризму, состоявшую из двух параллельных пластин и тончайшей проволочки между ними. Диаметр проволочки был меньше одного микрона (одной миллионной части метра). Электроны рассеивались на этой проволочке и регистрировались по одному очень чувствительным детектором. В этом эксперименте роль двух щелей выполняли края проволочки.

Возникновение интерференционной картины показано на рис. 6.11. Вначале на экране монитора появляются всего несколько засвеченных точек, куда попадают электроны (рис. 6.11, а). По мере увеличения длительности эксперимента число точек на экране возрастает, кажется, что они расположены хаотично без какого-либо порядка (рис. 6.11, б
и в). Правда, уже на рис. 6.11, в возникает что-то похожее на интерференционные полосы. Четкие интерференционные полосы возникают примерно через 20 мин (рис. 6.11, г). Эти полосы сформированы из ярких точек, каждая из которых соответствует одному электрону, попавшему в детектор. Поскольку в каждый момент в приборе находится только один электрон, такая интерференционная картина может получиться, если считать, что «электронная волна» огибает проволоку одновременно с двух сторон.

Рис. 6.11. Возникновение интерференционной картины в эксперименте
фирмы Hitachi

Самое интересное во всей этой истории то, что такая же интерференционная картина получится, если вместо фотонов или электронов мы возьмем протоны, нейтроны, которые примерно в 2000 раз тяжелее электрона, или еще более тяжелые частицы, например атом углерода или молекулу фуллерена, содержащую 60 атомов углерода. Интерференционные эксперименты, проделанные со всеми этими частицами, показали, что волновая природа поведения присуща не только электрону и фотону, но является неотъемлемым свойством вещества. Однако чем тяжелее частица, тем сложнее экспериментально выявить ее волновые свойства. Вот почему в обыденной жизни мы не замечаем этих свойств, так как нас окружают тела в неизмеримое число раз массивнее, чем рассмотренные выше частицы.

Литература

Фейнман Р. КЭД – странная теория света и вещества. – М.: Наука, 1988.

Фейнман Р. Характер физических законов. – М.: Наука, 1987.

Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. – В 9 т. – т. 3: Излучение, волны, кванты. – М.: Мир, 1967
(гл. 37, 38).

Фабрикант В.А. О наблюдении дифракции поочередно летящих электронов // 50 лет квантовой механике. – М.: Наука, 1979. – с. 95.

Rodgers P. The double slit experiment // Phys. World. – 2002. –Sept.