Классическая концепция пространства и времени

Классическая механика основана на представлении об абсолютном трехмерном пространстве, существующем независимо от содержащихся в нем материальных объектов и подчиняющемся законам евклидовой геометрии, и о времени как о самостоятельном измерении, которое носит абсолютный характер и течет с одинаковой скоростью независимо от материального мира. Размеры тел, их массы, а также длительность событий одинаковы с точки зрения любого наблюдателя.

Евклидова геометрия.Греческий математикЕвклид жил в III в. до нашей эры. Он подытожил и систематизировал математические знания своих предшественников и в своем знаменитом сочинении «Начала» изложил геометрию, описывающую метрические свойства пространства, которое современная наука называет евклидовым.

Евклид придал математическую определенность атомистической идее пустого пространства, в котором движутся атомы. Простейшим геометрическим объектом у Евклида является точка, которую он определил как то, что не имеет частей. Другими словами точка – это неделимый атом пространства. Формирование понятий евклидовой геометрии связано также с наглядными представлениями об окружающем мире: например, прямые линии – натянутые нити. Евклидово пространство пустое, безграничное, изотропное, имеющее три измерения.

Евклидова геометрия основана на пяти постулатах. Бесконечность пространства характеризуется первыми тремя постулатами:

«От всякой точки до всякой точки можно провести прямую линию».

«Ограниченную прямую можно непрерывно продолжить по прямой».

«Из всякого центра и всяким раствором может быть описан круг».

Четвертый постулат, или аксиома о параллельных: «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной, т. е. ее не пересекающую».

Знаменитый пятый постулат: «Если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти две прямые встретятся с одной стороны, где углы меньше двух прямых».

Четвертый и пятый постулаты определяют свойства евклидова пространства и его геометрию, отличную от неевклидовых геометрий. Несколько позже Архимед установил еще одно свойство евклидова пространства: «Из всех линий, имеющих одни и те же концы, прямая будет наименьшей». Евклидово пространство плоское. Прямая линия в евклидовой геометрии является геодезической линией, т. е. линией, имеющей наименьшую длину. Движение тела по инерции (с постоянной скоростью) происходит вдоль геодезической линии.

«Начала» Евклида установили эталон для последующего естественно-научного и математического мышления. До двадцатого века «Начала» Евклида использовались в европейских школах в качестве учебника, и на протяжении более чем двух тысячелетий считалось, что такая геометрия отражает истинную сущность пространства.

Механика Ньютона.Становление классической физики неразрывно связано с именем выдающегося английского ученого Исаака Ньютона. Ньютон построил первую научную картину мира – классическую механику, опираясь на весь предшествующий опыт ученых: «Если я видел дальше других, то потому, что стоял на плечах гигантов». В 1687 г. вышел в свет фундаментальный научный труд Ньютона «Математические начала натуральной философии». По словам С.И. Вавилова, «в истории естествознания не было события более крупного, чем появление «Начал» Ньютона. Ньютоново учение о пространстве, времени, массах и силах давало общую схему для решения любых конкретных задач механики, физики и астрономии. Величественный пример системы мира, разработанный Ньютоном, увенчанный открытием всемирного тяготения, увлекал науку на новый путь, на применение ньютоновской схемы ко всем разделам физики. Возникла классическая физика по образцу и подобию «Начал».

Развивая представления древнегреческих атомистов, Ньютон рассматривал пространство и время как самостоятельные сущности, не зависящие друг от друга и от протекающих в них процессов, имеющих одинаковые свойства во всех системах отсчета (т. е. с точки зрения любого наблюдателя).

«Время, пространство, место и движение составляют понятия общеизвестные. Однако необходимо заметить, что эти понятия обыкновенно относятся к тому, что постигается нашими чувствами. Отсюда происходят некоторые неправильные суждения, для устранения которых необходимо вышеприведенные понятия разделить на абсолютные и относительные, истинные и кажущиеся, математические и обыденные.

I. Абсолютное, истинное, математическое время само по себе и по своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью.

Относительное, кажущееся, или обыденное, время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как-то: час, день, месяц, год.

II. Абсолютное пространство по самой своей сущности, безотносительно к чему-либо внешнему, остается всегда одинаковым и неподвижным.

Относительное [пространство] есть его мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное…

III. Место есть часть пространства, занимаемая телом, и по отношению к пространству бывает или абсолютным, или относительным. Положение… само по себе не есть место, а принадлежащее месту свойство. Движение целого то же самое, что совокупность движений частей его…

IV. Абсолютное движение есть перемещение тела из одного абсолютного его места в другое, относительное – из относительного в относительное же. Так, на корабле, идущем под парусами, относительное место тела есть та часть корабля, в котором тело находится <…> и которая, следовательно, движется вместе с кораблем. Относительный покой есть пребывание тела в той же самой области корабля <…>

Истинный покой есть пребывание тела в той же самой части того неподвижного пространства, в котором движется корабль со всем в нем находящемся. Таким образом, если бы Земля на самом деле покоилась, то тело, которое по отношению к кораблю находится в покое, двигалось бы с той абсолютной скоростью, с какой корабль идет относительно Земли. Если же сама Земля движется, то истинное абсолютное движение тела найдется по истинному движению Земли в неподвижном пространстве и по относительному движению корабля по отношению к Земле и тела по отношению к кораблю».

Характеристики движения.Механическое движение – простейшая форма движения материи. Оно состоит в изменении положения тела в пространстве относительно других тел с течением времени.

Для описания механического движения вводятся следующие понятия.

Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи. Это возможно, когда:

1) размеры тела намного меньше измеряемых расстояний;

2) тело движется поступательно, т. е. все точки тела движутся одинаково, любая прямая в процессе движения параллельна самой себе.

Система отсчета – средство для наблюдения за движением. Понятие движения относительно. Мы можем говорить о движении тела только по отношению к какому-то другому телу. Система отсчета (рис. 7.1) включает в себя:

1) тело отсчета, относительно которого рассматривается движение;

2) систему координат с осями x, y, z;

3) прибор для измерения времени (часы).

Радиус-векторrматериальной точки однозначно определяет ее положение в выбранной системе отсчета в данный момент времени. Координаты его конца x, y, z.

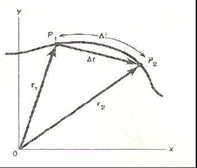
Рис. 7.1. Радиусы-векторы r₁ и r₂, путь dl и перемещение Dr материальной точки в плоскости XOY

Траектория – линия, «след», который оставляет конец радиуса-век-тора материальной точки в процессе ее движения.

Путьравен длине отрезка траектории между начальным и конечным положениями материальной точки.

Перемещение Dr– вектор, соединяющий начальную точку траектории с конечной. Его модуль (длина) дает кратчайшее расстояние между начальной и конечной точками траектории.

Скорость характеризует быстроту движения. Мгновенная скорость тела в данный момент времени в данной точке траектории – векторная величина, равная пределу отношения перемещения к промежутку времени, за которое это перемещение произошло. Другими словами, это первая производная перемещения по времени. Если тело движется вдоль оси x, то скорость находится как первая производная координаты:

.

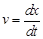Модуль скорости измеряется в метрах, деленных на секунду (м/с), и равен расстоянию, проходимому телом за 1 с.

Ускорениехарактеризует быстроту изменения скорости тела при неравномерном движении. Ускорение определяется как первая производная скорости по времени:

.

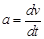Модуль ускорения измеряется в метрах, деленных на секунду в квадрате (м/с²) и равен изменению скорости за 1 с.

Масса m. Физическая величина, являющаяся мерой инертности тела в поступательном движении, называется инертной массой. Инертностью называется свойство тела сохранять свою скорость при отсутствии взаимодействия с другими телами. Масса тела измеряется в килограммах (кг).

Силой F называется векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел. Сила полностью определена, если заданы ее модуль, направление и точка приложения. Прямая линия, вдоль которой направлена сила, называется линией действия силы. Модуль силы измеряется в ньютонах (Н). Сила, с которой сразу несколько тел действует на данное тело (равнодействующая сила), равна векторной сумме сил, с которыми эти тела действуют на него по отдельности:

F = F₁ + F₂ + …

Это утверждение называется принципом независимости взаимодействий, или принципом суперпозиции сил.

Законы движения.Основная задача механики состоит в следующем: зная массу тела и действующие на него силы, найти ускорение, чтобы в любой момент времени уметь рассчитать скорость движения, положение тела в пространстве и построить траекторию движения в системе отсчета. Решение такой задачи основано на приведенных выше определениях характеристик движения и на законах движения, сформулированных ньютоном в его «Началах».

Закон I, или закон инерции, установлен еще Галилеем, но общую формулировку ему дал Ньютон: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока оно не понуждается приложенными силами изменять это состояние».

Системы отсчета, в которых свободное от воздействий тело движется по инерции, называют инерциальными системами отсчета (ИСО). При движении по инерции вектор скорости тела остается постоянным (v= const). Покой является частным случаем движения по инерции. Системы отсчета, связанные с землей, а также движущиеся с постоянной скоростью относительно земли, являются инерциальными.

Системы отсчета, в которых свободное тело не сохраняет скорость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением относительно любой инерциальной системы отсчета. Например, автомобиль во время разгона и торможения – неинерциальная система отсчета, а во время равномерного движения – инерциальная.

Закон II устанавливает причину изменения движения: «Изменение количества движения (импульса и, следовательно, скорости) пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует».

Согласно этому закону, под действием силы тело получает ускорение, прямо пропорциональное силе и обратно пропорциональное массе:

.

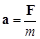Второй закон Ньютона дает нам уравнение движения тела F =ma и позволяет решить основную задачу механики. На основе этого закона устанавливается единица измерения силы: 1 ньютон (1 Н) – это сила, которая телу массой 1 кг сообщает ускорение 1 м/с².

Мы наблюдаем, что автомобиль с выключенным двигателем останавливается, а не продолжает двигаться с постоянной скоростью. По второму закону Ньютона на автомобиль должна действовать тормозящая сила, которой на практике является сопротивление воздуха и трение автомобильных шин о поверхность шоссе. Они сообщают автомобилю отрицательное ускорение до тех пор, пока он не остановится.

Закон III говорит о том, что не бывает односторонних действий: «Действию всегда есть равное и противоположное противодействие, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны».

Силы действия и противодействия приложены к разным телам и поэтому не могут уравновешивать друг друга. Каждое тело получает свое ускорение. Отношение модулей ускорений взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Тяжелое тело получает меньшее ускорение, а легкое – большее.

Порядок решения прямой задачи динамики состоит в следующем.

1. Выясняем, какие силы действуют на тело, записываем второй закон Ньютона и находим ускорение.

2. Зная ускорение a и начальные условия (т. е. значения характеристик движения v₀ и x₀ в некоторый момент времени, условно принятый за начальный), мы можем, используя формулы-определения, в любой момент времени вычислить скорость, координаты материальной точки и построить траекторию в системе отсчета:

v = 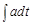, x = .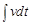

Принцип причинности.Человечество всегда волновали следующие вопросы.

каков мир: упорядочен и познаваем или хаотичен и неопре-делен?

как происходят события: все обусловлено причиною или все происходит случайно? В конечном счете, речь идет о том, существует ли свобода выбора (свобода воли) для объекта.

Научная теория Ньютона рисует образ мира в виде сложного механизма, работа которого подчинена законам механики. В мире Ньютона любое состояние объекта можно точно рассчитать, все обусловлено причиной и не может быть случайным. Пьер Симон Лаплас (1749–1827) – французский математик, физик и астроном выдвинул идею «мирового дифференциального уравнения», описывающего движение и взаимодействие всех частиц, составляющих Вселенную. В его труде «Опыт философии и теории вероятностей» говорится о том, что, зная условия для одного момента времени, можно точно определить состояние любой частицы в любой другой момент времени. Другими словами, можно совершенно точно и однозначно рассчитать состояние всех частиц и предсказать будущее Вселенной.

Позицию научного детерминизма определил Эрнст Геккель в 1899 г. в труде «Мировые загадки». Он утверждает, что все, в том числе и мышление, есть порождение материального мира, полностью управляемого и обусловливаемого определенными законами. Свобода выбора – это иллюзия.

Научный детерминизм отражает как успехи классической науки конца XIX в., так и ее пределы. Дальнейшее развитие науки показало, что многие явления (поведение элементарных частиц, генетические мутации) носят случайный характер. Вычисление вероятностей состояний объектов заменило строгую предсказуемость.

Принцип относительности Галилея.В 1632 г. итальянский ученый Галилео Галилей написал сочинение «Диалог о двух главнейших системах мира: Галилеевой и Коперника», где он обосновал физическую эквивалентность инерциальных систем отсчета относительно протекающих в них процессов. «Уединитесь с кем-нибудь из друзей в просторное помещение под палубой корабля, запаситесь мухами, бабочками и другими мелкими летающими насекомыми. Пусть будет у вас также большой сосуд с водой и плавающими в нем маленькими рыбками. Подвесьте наверху ведерко, из которого вода будет падать капля за каплей в другой сосуд с узким горлышком, подставленный снизу. Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы будут плавать безразлично во всех направлениях; все падающие капли попадут в подставленный сосуд, и вам, бросая какой-нибудь предмет, не придется бросать его с большей силой в одну сторону, чем в другую; и если вы будете прыгать двумя ногами, то сделаете прыжок на одинаковые расстояния в любом направлении. Заставьте теперь корабль двигаться с любой скоростью, и тогда (если только его движение будет равномерным и без качки) во всех явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно».

Принцип относительности Галилея заключается в следующем: механические явления протекают одинаково во всех инерциальных системах отсчета, никакими опытами внутри ИСО нельзя установить, движется она или покоится. Следовательно, законы механики должны иметь одинаковый математический вид во всех ИСО.

Рассмотрим две инерциальные системы отсчета, движущиеся друг относительно друга с постоянной скоростью (рис. 7.2). В начальный

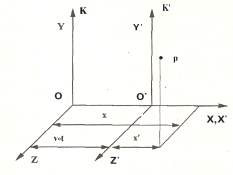
Рис. 7.2. Две системы отсчета, движущиеся относительно друг друга с посто-
янной скоростью v₀

момент времени их начала совпадают. Пусть система K условно неподвижна, а система K¢ движется относительно нее равномерно и прямолинейно со скоростью v вдоль оси OX. В некоторый момент времени t координаты движущейся материальной точки в разных ИСО будут отличаться, но они связаны определенным образом – согласно формулам, которые называют преобразованиями Галилея для координат и времени:

x = x¢ + Vt, y = y, z = z, t = t¢.

Продифференцировав эти выражения по времени, получим классическое правило сложения скоростей:

v = v¢ + V.

Скорость тела относительно подвижной инерциальной системы отсчета равна сумме скорости тела относительно неподвижной ИСО и скорости самой подвижной ИСО.

Повторное дифференцирование приводит к инвариантности (неизменяемости при переходе из одной системы отсчета в другую) ускорения:

a = a¢.

Поскольку масса одинакова в разных ИСО (m = m¢), получаем инвариантность второго закона Ньютона.