Релятивистская концепция пространства-времени. Кризис классической механики
Всякая физическая теория имеет свои границы применимости. За пределами этих границ теория перестает работать, ее оценки и предсказания не согласуются с результатами наблюдений и экспериментов. Тогда, согласно принципу соответствия, рождается новая теория, претендующая на более широкую область применения и включающая старую теорию как частный предельный случай.
Теория Ньютона подходит для описания движения тел со скоростями, далекими от скорости света (v << с). Законы классической механики дают прекрасные результаты, когда мы решаем задачи о движении планет, космических кораблей, снарядов, автомобилей и т. п. Но эти законы приводят к неправильным результатам, если их применить к объектам, движущимся со скоростью света или близкой к ней.
В середине XIX в. благодаря усилиям многих ученых, в особенности англичанина Майкла Фарадея и шотландца Джеймса Клерка Максвелла, была создана классическая электродинамика. Все электрические и магнитные явления Максвелл объединил в рамках единого математического описания. Согласно теории Максвелла, свет представляет собой электромагнитную волну, которая распространяется с постоянной скоростью с = 3×108 м/с = 300 000 км/с = 1,08 млрд км/ч. При такой скорости за 1 с можно обогнуть земной шар более семи раз. Большинство ученых считало, что световые волны должны распространяться в особой среде (эфире) подобно тому, как звуковые волны распространяются в воздухе. Если бы эфир существовал, то покоящаяся по отношению к нему система отсчета была бы выделенной, абсолютной. Только в этой системе отсчета скорость света действительно равнялась бы с. Для наблюдателя, движущегося со скоростью v относительно эфира по направлению от источника света или по направлению к источнику, скорость света, в соответствии с классическим правилом сложения скоростей, была бы равна (c – v) < c или (c + v) > c. Однако результаты экспериментов свидетельствовали о независимости скорости распространения света от скорости источника или наблюдателя.
В 1887 г. Альберт Майкельсон (который впоследствии стал первым американским лауреатом Нобелевской премии по физике) и Эдвард Морли выполнили очень тонкий и трудный эксперимент в Школе прикладных наук в Кливленде. Они решили воспользоваться тем, что раз Земля обращается вокруг Солнца со скоростью около 30 км/с, то и их лаборатория должна двигаться через эфир с этой относительно высокой скоростью. Конечно, никто не знал, перемещается ли эфир относительно Солнца, а если да, то в каком направлении и с какой скоростью. Но, повторяя измерения в разное время года, когда Земля находится в разных точках орбиты, они надеялись учесть этот неизвестный фактор. Майкельсон и Морли разработали эксперимент, в котором скорость света в направлении движения земли через эфир (когда мы движемся в сторону источника света) сравнивалась со скоростью света под прямым углом к этому направлению (когда мы не приближаемся к источнику света). К несказанному удивлению, они обнаружили, что скорость в обоих направлениях в точности одинакова. Опыты Майкельсона и Морли – эмпирические факты, показавшие несостоятельность классической механики в области явлений, где движение объектов происходит со скоростью света.
В дальнейшем многолетние усилия физиков-экспериментаторов подтвердили, что скорость света одинакова относительно всех наблюдателей и не зависит от скорости движения источника. В 1913 г. голландский физик Виллем де Ситтер предположил, что для измерения влияния движения источника на скорость света можно использовать двойные звезды, которые вращаются одна вокруг другой с большой скоростью. Многочисленные эксперименты показали, что скорость света, излучаемого обеими звездами, одинакова.
 Специальная теория относительности.
Специальная теория относительности.
В шестнадцатилетнем возрасте Альберт Эйнштейн осознал существование противоречия, которое в зародыше содержало в себе теорию относительности. Он попытался мысленно представить себе, каким бы увидел луч света наблюдатель, передвигающийся вместе с лучом со скоростью света. С одной стороны, интуиция и выводы классической механики Ньютона подсказывают, что световой луч должен оказаться неподвижным относительно наблюдателя. С другой стороны, согласно теории Максвелла, свет представляет собой электромагнитную волну, которая никогда не останавливается и не замедляется, такого явления, как неподвижный свет, в природе не существует. Возникший парадокс невозможно было разрешить, пользуясь законами классической физики.
Эйнштейн приветствовал эмпирическое подтверждение постоянства скорости света, поскольку оно позволяло разрешить мучившее его противоречие: с какой бы скоростью вы ни двигались за лучом света, он всегда будет удаляться от вас со скоростью света.
Скорость движения является мерой того, на какое расстояние может переместиться объект в течение заданного промежутка времени, например за одну секунду или за один час. Расстояние представляет собой характеристику пространства, а длительность – времени. Следовательно, скорость связывает понятия пространства и времени. Поэтому любой факт, который не укладывается в обычные представления о скорости движения (например, постоянство скорости света), может привести к пересмотру общих представлений о пространстве и времени.
В июне 1905 г. Эйнштейн, работавший в то время служащим патентного бюро в швейцарском городе Берне, послал в немецкий журнал Annalen der Physik статью под названием «К электродинамике движущихся сред». В ней разрешалось противоречие с лучом света на основе новых представлений о пространстве-времени, получивших название специальной теории относительности. Эйнштейн показал, что понятия пространства и времени, которые раньше казались независимыми и абсолютными, на самом деле тесно взаимосвязаны и являются относительными. Ключевым моментом в специальной теории относительности является понимание того, что наблюдатели, которые движутся по отношению друг к другу, будут по-разному воспринимать пространство и время: у них синхронизованные часы идут с разной скоростью, а один и тот же предмет имеет разные размеры. Причем это не связано с точностью измерительных приборов или ошибками при их использовании, а обусловлено свойствами пространства и времени.
Постулаты специальной теории относительности. В основе специальной теории относительности лежат два утверждения. Одно отражает универсальный характер скорости света, а другое – фундаментальную симметрию природы, связанную с протеканием процессов в различных системах
Постоянство скорости света.Все рассуждения теории относительности основаны напризнании факта постоянства скорости света, возведенного в ранг постулата. Скорость света постоянна во всех инерциальных системах отсчета (с = 3·108 м/с) и не зависит от движения источника. Это предельная скорость распространения сигнала, допустимая в природе.
Принцип относительности. Эйнштейн перенес принцип относительности Галилея на более широкий круг явлений. Любые физические явления (механические, электромагнитные) подчиняются одним и тем же законам во всех инерциальных системах отсчета, следовательно, физические законы должны иметь одинаковый математический вид во всех инерциальных системах отсчета.
Сущность принципа относительности состоит в том, что законы физики, каковы бы они ни были, должны быть абсолютно одинаковы для всех наблюдателей, совершающих равномерное прямолинейное движение. Таким образом, принцип относительности устанавливает полную симметрию между всеми наблюдателями, движущимися равномерно и прямолинейно. Если такие наблюдатели проводят серии одинаковых экспериментов, все используемое ими оборудование одинаково и нет никаких различий в условиях экспериментов, то ни сами наблюдатели, ни проводимые ими эксперименты никоим образом не будут зависеть от равномерного движения и будут получены одинаковые результаты. Аналогично законы физики, которые каждый из них будет выводить из результатов экспериментов, также будут идентичны.
Преобразования Лоренца.Физические законы сохраняют математический вид, если к ним применять преобразования Лоренца. В формулах преобразований координат и времени при переходе из одной системы отсчета в другую присутствует релятивистский параметр, зависящий от скорости:
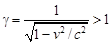 .
.
Переход из K¢ в K: Переход из K в K¢:
x = g (x¢ + vt¢), x¢ = g (x - vt),
y = y¢, y¢ = y,
z = z¢, z¢ = z,
t = g (t¢ + vx¢/c2). t¢ = g (t - vx /c2).
Анализируя преобразования Лоренца, можно сделать следующие выводы.
1. Пространственные параметры (x, y, z) и временной параметр t математически связаны друг с другом. Это отражает тот факт, что пространство и время неразделимы, образуют единое четырехмерное пространство-время, в котором происходят все физические явления.
2. Результаты измерения координат и времени зависят от относительной скорости движения объектов и наблюдателей. Для каждого наблюдателя существует свое «местное» время.
3. Соблюдается преемственность старых и новых теорий по принципу соответствия. При малых скоростях g = 1 и формулы преобразований Лоренца переходят в формулы преобразований Галилея. Теория относительности Эйнштейна включает в себя классическую механику как частный предельный случай.
4. При v > c подкоренные выражения становятся отрицательными и формулы теряют физический смысл. Это соответствует тому факту, что движение тел со скоростью, большей скорости света, в вакууме невозможно. Нельзя также пользоваться системой отсчета, движущейся со скоростью v = c, при этом подкоренные выражения превращаются в нуль и формулы также теряют физический смысл. Это значит, что с фотоном, движущимся со скоростью света с, принципиально не может быть связана система отсчета, в которой фотон был бы неподвижен: фотон (и другие безмассовые частицы) всегда движется со скоростью света.
Следствия специальной теории относительности.В классической механике одно и то же событие происходит одновременно во всех инерциальных системах отсчета, длительности процессов и размеры тел также одинаковы. В теории Эйнштейна понятия одновременности, длительности и протяженности принимают относительный характер.
Относительность одновременности. В классической механике одновременность событий является универсальным понятием, которое воспринимается всеми одинаково независимо от состояния движения. Постоянство скорости света, постулируемое Эйнштейном, приводит к тому, что понятие одновременности принимает относительный характер.
Мысленно представим себе равномерно движущийся вагон, в центре которого находится наблюдатель (пассажир). На платформе точно под фонарем, который выключен, находится другой наблюдатель (дежурный по станции). В тот момент, когда пассажир поравнялся с дежурным, зажигается фонарь и свет движется к передней и задней стенкам вагона. С точки зрения пассажира, свет в обоих направлениях движется с одинаковой скоростью и проходит одинаковые расстояния, поэтому достигает передней и задней стенок вагона одновременно.
С точки зрения дежурного, эти два события происходят не одновременно именно потому, что скорость света остается неизменной. Сначала свет достигает задней стенки, которая приближалась к нему. Несколько позже свет достигает передней стенки, которая удалялась от него. Таким образом, одни и те же события могут оказаться как одновременными, так и неодновременными относительно разных наблюдателей.
Если бы вагон имел длину 30 м, а поезд двигался со скоростью 16 км/ч, то, с точки зрения дежурного на платформе, свет достиг бы задней стенки вагона на одну миллионную одной миллиардной, т. е. на 10–15 доли секунды, раньше, чем он достиг бы передней стенки. Это различие действительно существует, но оно столь мало, что не может быть обнаружено непосредственно с помощью человеческих чувств. Если бы поезд двигался со скоростью 270 000 км/ч, то свет достиг бы задней стенки за время в 20 раз меньше. При высоких скоростях эффекты специальной теории относительности становятся все более заметными.
Замедление времени при движении. Рассмотрим, как движение влияет на течение времени (на ход часов). Пусть в точке с координатой х¢ в K¢-системе отсчета протекает некоторый процесс, например рождение и гибель частицы. Длительность процесса в этой системе Dt0 =
= t¢2 – t¢1 (собственное время жизни частицы, измеренное по ее собственным часам, т. е. по часам, которые относительно нее покоятся). Найдем длительность данного процесса Dt = t2 – t1 в K-системе, относительно которой K¢-система движется (по часам, движущимся относительно нашей частицы). Так как процесс происходит в точке с фиксированной координатой х¢ в K¢-системе, удобно воспользоваться с этой целью преобразованиями Лоренца для времени t = g (t¢ + vx¢/c2):
Dt = t2 – t1 = g (t2 – t1 ) = g Dt0 .
Отсюда видно, что длительность одного и того же процесса различна в разных инерциальных системах отсчета. В K-системе его длительность больше, а следовательно, в этой системе отсчета он протекает медленнее. Часы, движущиеся относительно частицы, идут медленнее, чем ее собственные неподвижные часы. Собственное время жизни частицы – самое короткое.
Таким образом, течение времени зависит от состояния движения. Не существует единого мирового времени. Понятие длительности события является относительным, оно приобретает смысл только тогда, когда указано, к какой системе отсчета это относится.
Эффект замедления времени является симметричным относительно обеих инерциальных систем отсчета. Если, с точки зрения наблюдателя, находящегося в K-системе, медленнее идут часы в K¢-системе, то, с точки зрения наблюдателя, находящегося в K¢-системе, медленнее идут часы в K-системе, т. е. сами наблюдатели не замечают замедления хода своих часов.
Замедление хода движущихся часов – следствие инвариантности скорости света, оно не может быть приписано какому-либо изменению в свойствах часов, обусловленному их движением.
Сокращение длины в направлении движения. Чтобы понять, в чем выражается влияние движения на пространство, сравним длину предмета, когда он покоится и когда движется. Расположим неподвижный в K¢-системе стержень вдоль оси х¢, т. е. вдоль направления движения этой системы отсчета относительно K-системы. Пусть длина неподвижного стержня в K¢-системе L0 = х2¢ – х2¢ (собственная длина). В
K-системе, относительно которой стержень движется, его длину определяют как расстояние L между координатами х2 и х1 его концов, взятыми в один и тот же момент времени (t2 = t1). Воспользовавшись преобразованиями Лоренца для координат x = g (x¢ + vt¢), запишем
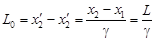 .
.
Таким образом, длина – понятие относительное, имеющее смысл только по отношению к той или другой системе отсчета. Наибольшее значение имеет собственная длина объекта, т. е. длина, измеренная по линейке, покоящейся относительно объекта. Наблюдатели в разных инерциальных системах отсчета обнаруживают сокращение в g раз длины движущегося объекта в направлении его движения. Можно ли в таком случае ставить вопрос: какая длина является действительной?
И если длина стержня сокращается, то в чем заключается причина, вызывающая такое изменение?
Макс Борн предлагает разобраться с этими вопросами на наглядном примере: «Когда я отрезаю от колбасы один ломтик, он будет большим или меньшим в зависимости от того, насколько я скашиваю при резке нож. Совершенно бессмысленно говорить о различных величинах ломтиков колбасы как о кажущихся и считать минимальную их длину при отвесном положении ножа действительной величиной». Подобно тому, как мы получаем ломтики колбасы разной длины в зависимости от положения ножа, длина стержня оказывается большей или меньшей в зависимости от движения наблюдателя. Сокращение длины зависит лишь от способа наблюдения, т. е. от характеристик движения той системы, в которой производится измерение.
Эффект сокращения размеров, как и эффект замедления времени, является симметричным. Если сравнивать два движущихся относительно друг друга стержня, собственная длина которых одинакова, то с точки зрения каждого из них длина другого стержня будет короче, причем в одинаковых отношениях. Сами стержни «не замечают» сокращения своей длины.
Из определения длины, приведенного выше, следует, что сокращение длины стержня (как и размеров любого другого объекта в направлении движения) является следствием относительности понятия одновременности. Оно вовсе не обусловлено тем, что внутри объекта возникают какие-либо напряжения, вызывающие деформацию.
Итак, сокращение размеров тел в направлении их движения и замедление времени представляют собой реальный и объективный факт, не связанный с какими-либо иллюзиями наблюдателя. Все значения размеров тела или промежутков времени, полученные в разных системах отсчета, являются равноправными, т. е. все они правильные.
Эйнштейн создал свою теорию более ста лет назад, но большинство людей воспринимает пространство и время как абсолютные понятия. Интуитивно мы не чувствуем специальной теории относительности, поскольку не имеем подкрепления в рамках своего жизненного опыта из-за того, что величина релятивистских эффектов зависит от скорости движения. Различия в восприятии пространства и времени между неподвижным наблюдателем и наблюдателями, едущими в машинах или летящими в самолетах, безусловно, существуют, но они столь малы, что остаются незамеченными.
В действительности же понятия длины и промежутков времени столь же относительны, как понятия движения и покоя.
Энергия и масса.Эйнштейн выяснил, что взаимосвязаны не только пространство и время, но и такие физические характеристики мироздания, как масса и энергия. Если известны масса тела m и скорость его движения v, то можно вычислить полную энергию тела:
E = g mc2.
Полная энергия тела включает в себя энергию покоя и энергию движения (кинетическую). В полную энергию не включена потенциальная энергия тела во внешнем поле (если таковое действует на тело):
E = E0 + Eкин .
Энергия покоя является еще одним инвариантом теории относительности, она равна произведению массы тела на квадрат скорости света:
E0 = mc2.
Кинетическую энергию получим как разность полной энергии и энергии покоя:
Eкин = E – E0 = (g – 1) mc2.
Во-первых, взаимосвязь массы с энергией означает, что даже небольшое уменьшение массы сопровождается выделением большого количества энергии. На этом основано получение ядерной энергии. Например, если 1 мкг = 10–6 кг массы какого-либо вещества превратить в энергию, то мы получим около 1011 Дж = 10 000 МДж энергии. Во-вторых, это объясняет, почему невозможно движение физических тел со скоростью света. В классической механике, с одной стороны, есть инертная масса, характеризующая способность тела препятствовать изменению его скорости, с другой – лишенная инерции энергия. Начальная величина скорости не имеет значения. С точки зрения классической механики совершенно безразлично, начинается ли ускорение тела при скорости 100 м/с или же 290 000 км/с. Согласно теории относительности энергии, как и массе, присуще свойство инертности. Не только величина массы, но и начальная скорость влияют на ускорение тела. Чем быстрее движется тело, тем больше его кинетическая и полная энергия и тем труднее становится разгонять его дальше. При движении элементарной частицы – мюона со скоростью в 99,9 % от скорости света его энергия возрастает в 22 раза по сравнению с энергией покоя, при скорости в 99,999 % – в 224 раза, при скорости в 99,99999999 % – в 70 000 раз. Чтобы достичь светового рубежа, нужно затратить бесконечно большое количество энергии, что невозможно.
Мир Минковского.Немецкий математик Герман Минковский (1864–1909) создал математическую теорию физических процессов в четырехмерном мире. В 1908 г. в докладе «Пространство и время» и в статье «Основные уравнения для электродинамических процессов в движущихся телах» он дал наглядную геометрическую интерпретацию преобразованиям Лоренца. Выступая с докладом на 80-м съезде немецких естествоиспытателей и врачей в Кельне, он заявил: «Отныне пространство само по себе и время само по себе низводятся до роли теней, и лишь некоторый вид соединения обоих должен еще сохранить самостоятельность». Четырехмерное пространство-время с координатами (x, y, z, t) Минковский называет миром. Событие в пространстве Минковского изображается точкой. Совокупность точек образует мировую линию (рис. 7.3).
Относительный характер пространственных и временных промежутков отнюдь не означает, что теория относительности вообще отрицает существование каких бы то ни было абсолютных величин. В действительности дело обстоит как раз наоборот. Задача, которую ставит перед собой теория относительности, заключается в нахождении таких
|
| |
|
|
|
|
|
|
|
|
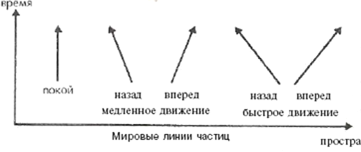
Рис. 7.3. Движение частиц в пространстве-времени
величин и законов, которые не зависели бы от выбора системы отсчета. Такими величинами являются универсальная скорость распространения взаимодействия, равная скорости света в вакууме, энергия покоя. Инвариантной величиной является также интервал между двумя событиями в четырехмерном пространстве-времени, квадрат которого определяется как
S2 = c2 Dt2 – 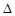 L2 = c2 Dt¢2 –
L2 = c2 Dt¢2 – 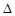 L¢2,
L¢2,
где 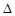 L2 =
L2 = 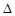 x2 +
x2 + 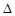 y2 +
y2 + 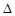 z2.
z2.
В релятивистской физике историю объекта (частицы) можно изобразить на пространственно-временной диаграмме (рис. 7.4). Здесь
| |
|
|
|
|
|
|
|

Рис. 7.4. Взаимодействие частиц (рассеяние фото-
на на электроне) в пространстве-времени
горизонтальная ось соответствует одному измерению пространства, двумя другими приходится пренебречь для того, чтобы можно было изобразить диаграмму на плоскости. Вертикальная ось соответствует времени. Путь частицы в пространстве-времени называют ее мировой линией. Если частица покоится, она тем не менее движется во времени, и ее мировая линия представляет собой вертикальную линию. Если частица перемещается в пространстве, ее мировая линия становится наклонной: чем выше скорость частицы, тем значительнее наклон мировой линии. Заметим, что во времени частицы могут перемещаться только вверх, в пространстве они способны перемещаться как вправо, так и влево.
При помощи пространственно-временных диаграмм в квантовой теории поля изображают процессы взаимодействия различных частиц. Рассмотрим процесс столкновения (рассеяния) электрона и фотона. Соответствующая диаграмма прочитывается следующим образом (снизу вверх согласно течению времени): электрон, обозначенный как е–1 (минус означает отрицательный заряд), сталкивается с фотоном, обозначенным как g (греческая буква гамма); электрон поглощает фотон и продолжает движение с несколько изменившейся скоростью (на диаграмме это отражается как изменение угла наклона мировой линии); через некоторое время электрон испускает фотон и восстанавливает первоначальное направление движения.
Дата добавления: 2015-01-15; просмотров: 2575;
