III.3.1. Геометрия и физика пространства и времени

Одной из наиболее известных теорем математики является теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов прилегающих к ней сторон (катетов) (рис. 1.7). Выполняется ли эта математическая истина также в реальном мире, изучаемом физикой? И может ли быть иначе? Одного умозаключения тут недостаточно, и для ответа мы должны обратиться к опыту.

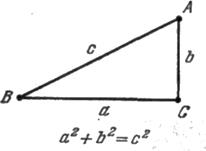
Рис. 1.7. Точно ли описывают физический мир аксиомы Евклидовой геометрии,

из которых логически выводится теорема Пифагора? Это может решить только опыт.

Приведем здесь некоторые соображения, отметив, что они имеют несколько неполный характер, так как мы пока не можем пользоваться метрикой трехмерного пространства, обладающего кривизной.

Вначале вообразим, в каком положении находились бы двумерные разумные существа, живущие в такой Вселенной, которая представляет собой поверхность шара. Математики «двумерного пространства» могли бы дать этим разумным существам описание свойств и других пространств, с тремя и даже большим числом измерений, но им так же трудно было бы представить в своем воображении такие вещи, как и нам — нарисовать себе четырёхмерное пространство.

Как же эти двумерные разумные существа могут установить, что живут на поверхности, обладающей кривизной? Чтобы убедиться в этом, им нужно проверить, что для данной поверхности теряют силу хотя бы некоторые аксиомы геометрии на плоскости, а для этого надо экспериментально установить, выполняются ли определенные теоремы евклидовой геометрии на той поверхности, на которой они живут.

Эти двумерные разумные существа будут проводить «прямые» линии как линии кратчайших расстояний между любыми двумя точками В и С на поверхности шара (рис. 1.8). Мы считали бы такую линию дугой большого круга. Они могут строить прямоугольные треугольники и проверять на них, выполняется ли теорема Пифагора. Для очень маленького треугольника, каждая из сторон которого мала по сравнению с радиусом шара, теорема будет выполняться с большой, но не с абсолютной точностью. Для большого треугольника обнаружится значительное отклонение от этой теоремы.

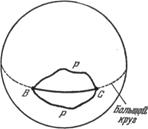
Рис. 1.8. Кратчайшее «прямолинейное» расстояние между точками В и С на шаровой

поверхности проходит по дуге большого круга, соединяющей эти точки,

а не по какому-либо другому пути Р.

Если В и С — точки на экваторе шара, то «прямая» линия, соединяющая их, является дугой ВС экватора (рис. 1.9). Кратчайшим путем из точки С на экваторе к северному полюсу А является линия постоянной долготы (меридиан), пересекающая экватор ВС под прямым углом.

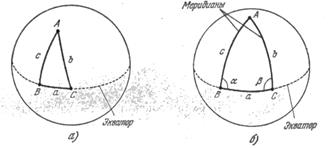
Рис. 1.9. Двумерные существа могли бы строить треугольники с заданными вершинами

А, В, С к отрезками «прямых» линий в качестве сторон. Они нашли бы, что для

маленьких прямоугольных треугольников а² + в² ≈ с² и сумма углов треугольника

немного больше 180° (а). Если бы они рассматривали большие треугольники, то сумма

углов все более превышала бы 180° (б). Здесь точки В и С находятся на экваторе, а точка

А — полюс шара, причем оба угла α и β прямые. Очевидно, что а² + в² ≠ с²,

потому что в=с.

Кратчайшим путем из А в В является отрезок другого меридиана, который также пересекает экватор ВС под прямым углом. Получается прямоугольный треугольник, в котором в=с. Очевидно, что на поверхности шара теорема Пифагора не выполняется, потому что с² не может быть здесь равно а² + в²; далее, сумма внутренних углов треугольника АВС всегда больше 180°. Измерения, сделанные на искривленной поверхности ее двумерными обитателями, дают им возможность убедиться, что эта поверхность действительно обладает кривизной.

Однако эти обитатели всегда могут сказать, что законы геометрии на плоскости точно описывают их двумерный мир, а причина указанного несоответствия связана со свойствами линеек, применяемых для измерения кратчайшего расстояния и определения «прямой» линии. Они могут показать, что метровые линейки не имеют постоянной длины, а растягиваются и сжимаются, когда их переносят в различные места поверхности. Только в результате непрерывных измерений, выполненных различными способами и давших одинаковый результат, становится очевидно, что наиболее простое объяснение нарушения евклидовой геометрии заключается в том, что поверхность имеет кривизну. Аксиомы геометрии на плоскости не являются в этом искривленном двумерном мире самоочевидными истинами; они воо6ще уже не являются истинами. Мы видим, что вопрос о том, какова истинная геометрия Вселенной, представляет собой физическую проблему, подлежащую экспериментальному исследованию. Описывая измерения, выполненные в нашем собственном трехмерном мире, мы обычно не задаем себе вопроса о том, справедлива ли евклидова геометрия, потому что евклидова геометрия является настолько, хорошим приближением к геометрии Вселенной, что при практических измерениях не обнаруживаются какие-либо отклонения от нее. Это не означает, что применимость евклидовой геометрии самоочевидна или что эта геометрия совершенно точно выполняется в мировом пространстве. Великий математик XIX в. Карл Фридрих Гаусс высказал предположение, что необходимо проверить отсутствие кривизны трехмерного пространства, следующее из геометрии Евклида, измеряя сумму внутренних углов большого треугольника (рис. 1.10); он понимал, что если трехмерное пространство обладает кривизной, то сумма углов достаточно большого треугольника должна заметно отличаться от 180°.

Гаусс использовал (1821—1823) геодезические приборы .для точного измерения треугольника, образованного вершинами гор Брокен, Хохехаген и Инзельберг в Германия.

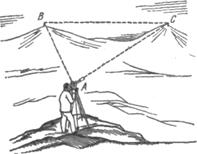
Рис. 1.10. Гаусс измерял углы треугольника, вершины которого находились

на вершинах трех гор, и в пределах точности своих измерений не обнаружил

отклонения суммы углов от 180°

Наибольшая сторона треугольника имела длину около 100 км. Измеренные внутренние углы были равны:

86° 13' 58,366^’’

53° 6' 45,642^’’

40° 39' 30,165^’’

Сумма 180° 00' 14,173^’’

В работах Гаусса нет данных по поводу оценки точности этих значений; вероятно, последние два десятичных знака не являются достоверными. Поскольку на каждой из трех вершин геодезические приборы устанавливались по местной плоскости горизонта, эти три горизонтальные плоскости не были параллельными. Вычисленную поправку, названную сферическим избытком и равную 14,853 дуговой секунды, надо вычесть из полученной суммы углов. Исправленная сумма, равная 179^o59',320^’’, отличается от 180° на 0,680 дуговой секунды. Гаусс считал, что эта величина находится в пределах ошибок измерений, и сделал вывод, что в пределах точности этих измерений пространство является евклидовым.

Из приведенного выше, примера очевидно, что евклидова геометрия дает правильное описание свойств маленького треугольника на обыкновенной двумерной сферической поверхности, а отклонения от евклидовой геометрии становятся все более значительными по мере увеличения размеров. Для того чтобы убедиться, что наше трехмерное физическое пространство действительно является плоским, нам надо произвести измерения с очень большими треугольниками, вершины которых образованы Землей и удаленными звездами или даже галактиками. Однако мы сталкиваемся с такой трудностью: наше положение определяется положением Земли, и мы еще не имеем возможности передвигаться в космическом пространстве с масштабными линейками, чтобы измерять стороны и углы астрономических треугольников.