Интерференционный опыт Юнга с электронами

Этот опыт теоретически подробно разобран в лекциях Фейнмана по физике4. Схема эксперимента показана на рис. 6.5^*.

В этом опыте пучок электронов от источника падает на экран, в котором имеется две щели – 1 и 2. За экраном вдоль стенки перемещается детектор, который регистрирует попадающие в него электроны. Число электронов, попадающее в детектор, скажем, за одну минуту, зависит от его положения (от координаты х вдоль стенки или от угла q). Обозначим это число N₁₂(x), где нижний индекс 12 означает, что открыты обе щели. Пусть за минуту источник испустил N электронов. Тогда величина P₁₂(x) = N₁₂(x)/N означает долю от общего числа электронов, попавших в точку x. Ее можно также интерпретировать как вероятность того, что электрон попадет в точку х. Эта зависимость изображена на рис. 6.5, б. Фактически это интерференционная кривая, и она точно совпадает с интерференционной кривой для опыта Юнга со светом (см. рис. 6.3).

Постараемся теперь понять поведение электронов с позиции «здравого смысла». Поскольку детектор регистрирует только электрон целиком, т. е. он не может зарегистрировать половину электрона, мы можем подумать, что для того чтобы электрон попал в детектор, он должен пройти либо через щель 1, либо через щель 2. Таким образом, все электроны, достигшие стенки, казалось, должны пройти либо через одну щель, либо через другую, т. е. кривая P₁₂ должна быть суммой кривых P₁ и P₂, соответствующих относительной доле электронов, прошедших либо через щель 1, либо через щель 2. Проверим это предположение.

Сначала закроем щель 2. При этом мы получим зависимость P₁ числа электронов от положения детектора (рис. 6.6^*). Перекроем теперь щель 1, а щель 2 оставим открытой. мы получим зависимость P₂ числа электронов от положения детектора, показанную рис. 6.7. Если же открыть обе щели и считать, что электрон проходит либо через щель 1, либо через щель 2, то мы должны получить зависимость 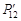, равную сумме графиков P₁ и P₂ ( 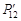= P₁ + P₂). Эта зависимость показана на рис. 6.8^*. Сравнение с рис. 6.5 показывает, что 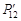¹ P₁₂. Иными словами, при обеих открытых щелях распределение P₁₂ не есть сумма P₁ и P₂ – распределений, описывающих прохождение электрона через конкретную щель.

Если к объяснению подходить интуитивно, с позиций «здравого смысла», то здесь, кажется, есть какая-то нестыковка. Мы ведь можем придумать такой эксперимент, чтобы определять, через какую щель электрон действительно прошел. Например, за экраном можно поставить источник света и около каждой щели за экраном поместить детекторы фотонов D1 и D2. (рис. 6.9^*). Как только электрон появляется за экраном около, скажем, щели 1, на нем рассеивается фотон и этот рассеянный фотон попадает в детектор D1. Таким образом, мы можем узнать, сколько электронов прошло через каждую щель. Самое интересное здесь то, что интерференционная картина получится такой же, как на рис. 6.8. Следовательно, как только мы знаем из измерений, через какую щель прошел электрон, интерференционная картина, показанная на рис. 6.5, не получится. Более того, если мы не проводим никаких измерений с целью выяснить, через какую щель прошел электрон, а просто считаем, что он прошел через одну из щелей, то, как мы показали выше, вместо интерференционной картины, приведенной на рис. 6.5, должно бы получиться распределение интенсивности, показанной на рис. 6.8 или 6.9. Но в действительности получается интерференционная картина, показанная на рис. 6.5. Поэтому мы не можем считать, что электрон проходит через одну из щелей. Этот вопрос просто не имеет смысла. Пока электрон не зарегистрирован, он ведет себя как волна. Электрон становится частицей только в момент регистрации его детектором. Как раз в этом и проявляется двойственный характер электрона. В этом смысле принято говорить о дуализме волна–частица.