Модель идеального смешения.

Модель, идеального смешения соответствует аппарату, в котором поступающее в него вещество мгновенно распределяется по всему объему аппарата. Концентрация вещества в любой точке аппарата равна концентрации на выходе из него.

Уравнение модели идеального смешения записывается в виде

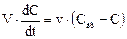
где С_вх — концентрация вещества на входе; С — концентрация вещества в аппарате и на выходе из аппарата; V — объем аппарата; υ — объемный расход потока через аппарат.

Отклик модели идеального смешения на входное возмущение для метода вымывания соответствует убывающей экспоненциальной зависимости с начальной концентрацией С_н (кривая 1 на рис. 1) :

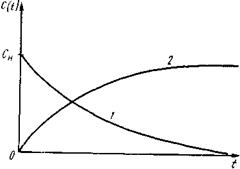
Рис. 1. Функции отклика для модели идеального смешения: 1 - метод вымывания (метод импульсного введения индикатора); 2 - метод ступенчатого введения индикатора него вытеснения.

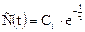
При импульсном возмущении уравнение имеет аналогичный вид. Так как введенный индикатор в количестве g мгновенно распределяется по всемуобъему и начинается его вымывание. Начальная концентрация при этом равна С_н = q/V. Соответственно изменение концентрации на выходе потока из аппарата описывается уравнением (кривая 1 на рис. 1).

При ступенчатом введении индикатора со скачкообразным изменением концентрации в момент времени t =0 от С = 0 до С = С_вх функция отклика принимает вид

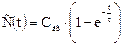
(кривая 2 на рис.1).

Передаточная функция аппарата идеального смешения определяется с помощью преобразования по Лапласу исходного уравнения модели и имеет вид

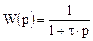
Отметим, что модель идеального смешения отличается значительной простотой. Вместе с тем в ряде случаев ее применение вполне обосновано. Это в первую очередь относится к интенсивно перемешиваемым аппаратам с отражательными перегородками (аппараты с мешалками, цилиндрические аппараты со сферическим дном, в условиях больших скоростей перемешивания и т. д.).