Основные числовые характеристики распределения элементов потока по времени пребывания в аппарате.
Расчет распределения времени пребывания частиц потока основан на статистическом понятии моментов и связан с распределением плотности вероятностей. Основные свойства распределения случайной величины можно описать несколькими числовыми характеристиками, которые определяют наиболее существенные особенности распределения. Такой системой характеристик являются моменты распределения случайной величины, которые систематизируются по трем признакам: по порядку β момента; по началу отсчета случайной величины; по виду случайной величины.
Порядок β момента может быть любым целым числом. Практически же рассматривают моменты нулевого, первого, второго, третьего и четвертого порядков, т.е. β = 0, 1, 2, 3,4. В зависимости от начала отсчета случайной величины различают начальные и центральные моменты. Общий вид начальных моментов функции распределения таков:
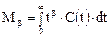
Каждый из моментов имеет определенный физический смысл. Нулевой момент - это площадь под кривой; первый момент - характеризует среднее значение (среднее время пребывания), или математическое ожидание случайной величины времени пребывания.
Случайные величины, отсчитываемые от математического ожидания, называются центрированными. Моменты центрированной величины называются центральными. Общий вид центральных моментов таков:
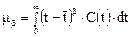
Второй центральный момент характеризует рассеяние случайной величины относительно среднего времени пребывания, он называется дисперсией и обозначается через σ2:

Третий центральный момент характеризует асимметрию распределения и равен
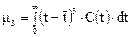
Четвертый центральный момент определяет островершинность распределения
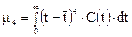 и т.д.
и т.д.
В силу стохастической природы движения элементов потока в аппарате их время пребывания является случайной величиной с некоторой плотностью распределения. Оценкой функции плотности распределения элементов потока по времени пребывания в аппарате может служить С-кривая, снимаемая на выходе аппарата при импульсном возмущении. Тогда моменты С-кривой являются основными характеристиками распределения элементов потока по времени пребывания, определяя тем самым структуру потока.
Рассмотрим теперь связь моментов нормированной и безразмерной С-кривой. Значения нормированной С-кривой определяются как
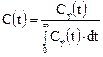
Начальный момент порядка β нормированной С-кривой есть
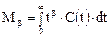
Дата добавления: 2015-03-03; просмотров: 1444;
