Метод импульсного возмущения.
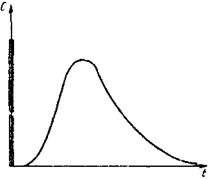
Рис. 1. Типичная функция отклика системы на импульсное возмущение
Импульсный метод. В соответствии с этим методом в поток на входе его в аппарат практически мгновенно, в виде дельта-функции, вводят определенное количество индикатора.
Допустим, что в поток на входе его в аппарат произвольной сложности ввели практически мгновенно индикатор и определили функцию отклика на это возмущение, изображенную на рис. 1, Обозначим объем аппарата через V и объемную скорость потока — через υ.
Количество индикатора, время пребывания которого в аппарате изменяется от t до t + dt, составляет
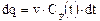 (1)
(1)
Отношение dq ко всему количеству индикатора q выражает долю индикатора, вышедшего из аппарата за время от t до t + dt:
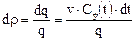 (2)
(2)
Так как поведение индикатора в аппарате идентично поведению основного потока, то выражение (1) представляет собой долю потока, время пребывания которого изменяется от t до t + dt.
Введем безразмерную концентрацию С (θ) по формуле:
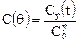 , где
, где 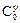 — начальная концентрация в потоке:
— начальная концентрация в потоке:
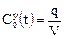
Одновременно введем безразмерное время θ по формуле
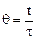
где 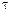 - среднее время пребывания частиц потока в аппарате:
- среднее время пребывания частиц потока в аппарате:
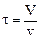
Теперь уравнение (2) можно привести к виду
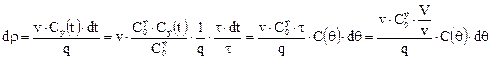 (3)
(3)
Общее количество введенного индикатора определяется выражением
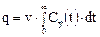
Тогда из уравнений (2), (3) следует
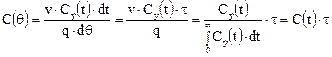
где выражение
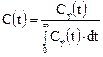
задает нормированную С-кривую.
Построим экспериментальную кривую в координатах С(θ), θ (рис. 2). Такая кривая называется С-кривой. Заштрихованная площадь под ней равна
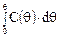
и означает долю потока, время пребывания которого в аппарате изменяется от 0 до б. Естественно, что
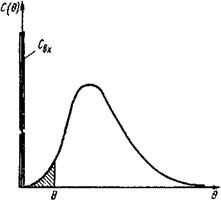
Рис. 2. Типичная С-кривая
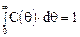
Таким образом, С-кривая является характеристикой распределения элементов потока по времени их пребывания в аппарате.
Среднее время пребывания потока в аппарате есть
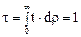
Поставим в это выражение значение dρ из уравнения (2) и воспользуемся тем, что 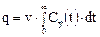 . Тогда получим
. Тогда получим
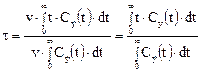
Дата добавления: 2015-03-03; просмотров: 1538;
