Дробные реплики от полного факторного эксперимента.
Если при получении уравнения можно ограничиться линейным приближением, то число опытов резко сокращается при использовании так называемых дробных реплик от полного факторного эксперимента или дробного факторного эксперимента (ДФЭ). Для того чтобы дробная реплика представляла собой ортогональный план, в качестве реплики следует брать ближайший полный факторный эксперимент. Число опытов при этом должно быть больше, чем число неизвестных коэффициентов в уравнении регрессии. Допустим, что нам нужно получить линейное приближение некоторого небольшого участка поверхности отклика при трех независимых факторах:
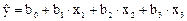
| N | х0 | х1 | х2 | х3 |
| +1 | +1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | |
| +1 | -1 | +1 | -1 | |
| +1 | +1 | -1 | -1 |
Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании для ПФЭ 22 использовать столбец x1 x2 в качестве плана для xз
| N | х0 | х1 | х2 | х1 х2 |
| +1 | +1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | |
| +1 | -1 | +1 | -1 | |
| +1 | +1 | -1 | -1 |
Такой сокращенный план—половина ПФЭ 23—носит название полуреплики от ПФЭ 23. Пользуясь таким планированием, можно оценить свободный член и три коэффициента уравнения регрессии при линейных членах.
На практике обычно не удается априори постулировать равенство нулю эффектов взаимодействия, однако часто имеются основания полагать, что некоторые из них малы по сравнению с линейными эффектами. Если коэффициенты регрессии при парных произведениях не равны нулю, то найденные нами коэффициенты будут смешанными оценками для генеральных коэффициентов:
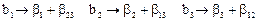
где β—математические ожидания для соответствующих коэффициентов.
Эти генеральные коэффициенты не могут быть раздельно оценены по плану, включающему всего четыре опыта, так как в этом случае неразличимы столбцы для линейных членов и парных произведений. Если, например, в дополнение к столбцам, приведенным в таблице, мы вычисляем еще столбец для произведения x1 x2, то увидим, что элементы этого столбца в точности равны элементам столбца х2. Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Для того чтобы определить, какие генеральные коэффициенты смешаны, удобно пользоваться таким приемом: поставив x3 на место x1 х2, получаем соотношение
x3 = x1 x2
называемое генерирующим соотношением. Умножим обе части генерирующего соотношения на x3.
При этом справа получим единичный столбец
1 = x1 x2 x3
Произведение носит название определяющего контраста, с его помощью удобно определять, в каких столбцах одинаковые элементы.
Умножив по очереди определяющий контраст на x1, x2, x3 находим:
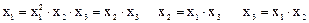
Полученным соотношениям соответствует система смешанных оценок.
При использовании дробного факторного эксперимента (ДФЭ) необходимо иметь четкое представление о так называемой разрешающей способности дробной, реплики, т. е. определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих генеральных коэффициентов. Тогда в зависимости от поставленной задачи подбирается дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента.
Например, в задаче с четырьмя факторами k = 4, в качестве генерирующего соотношения можно взять
x4 = x1 x2 x3
и любой из эффектов двойного взаимодействия, например
x4 = x1 x2
Матрица планирования с генерирующим соотношением приведена в табл.
| N | х0 | х1 | х2 | x3 | х4 |
| +1 | +1 | +1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | +1 | |
| +1 | -1 | +1 | +1 | -1 | |
| +1 | +1 | -1 | +1 | -1 | |
| +1 | +1 | +1 | -1 | -1 | |
| +1 | -1 | -1 | -1 | -1 | |
| +1 | -1 | +1 | -1 | +1 | |
| +1 | +1 | -1 | -1 | +1 |
Воспользовавшись определяющим контрастом 1 = x1 x2 x3 x4 при этом получаем такую систему совместных оценок:
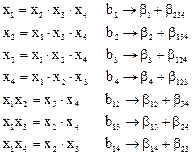
В реальных задачах тройные взаимодействия бывают равными нулю значительно чаще, чем двойные. Значит, если нас более всего по физическому смыслу задачи интересуют оценки для линейных эффектов, следует брать генерирующее соотношение
x4 = x1 x2 x3
При генерирующем соотношении матрица планирования имеет вид таблицы:
| N | х0 | х1 | х2 | x3 | х4 |
| +1 | +1 | +1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | +1 | |
| +1 | -1 | +1 | +1 | -1 | |
| +1 | +1 | -1 | +1 | -1 | |
| +1 | +1 | +1 | -1 | +1 | |
| +1 | -1 | -1 | -1 | +1 | |
| +1 | -1 | +1 | -1 | -1 | |
| +1 | +1 | -1 | -1 | -1 |
Определяющий контраст выражается соотношением
1 = x1 x2 x4
Получается следующая система оценок:
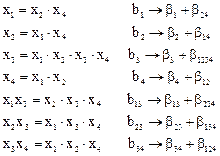
Следовательно, дробную реплику с генерирующим соотношением x4=x1 x2, имеет смысл использовать, если нас более всего интересуют коэффициенты β13 β23 β34. Применяют дробные реплики и большей степени дробности (1/4 реплики, 1/8 рецлики и т. п.). Дробную реплику, в которой р линейных эффектов приравнены к эффектам взаимодействия, обозначают 2k-p.
Таким образом, оптимальные двухуровневые планы имеют следующие преимущества: планы ортогональны и поэтому все вычисления просты; все коэффициенты определяются независимо друг от друга: каждый коэффициент определяется по результатам всех N опытов; все коэффициенты регрессии определяются с одинаковой и минимальной дисперсией. Необходимо также отметить, что линейные планы обладают свойством ротатабельности. Вследствие отсутствия корреляции между коэффициентами по закону сложения дисперсий в случае линейного уравнения для k факторов имеем:
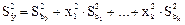
Так как Sbj2 = S2воспр/N, то
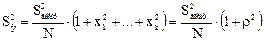
где ρ2—квадрат радиуса сферы в k-мерном пространстве.
Величину, обратную 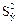 , можно принять за меру информации, содержащейся в уравнении регрессии.
, можно принять за меру информации, содержащейся в уравнении регрессии.
Согласно уравнению, количество информации убывает пропорционально квадрату радиуса сферы ρ2 и одинаково для всех эквидистатных точек. Планирование, обладающее таким свойством, называют ротатабельным планированием.
Описание «почти стационарной области».
В этой области становятся значимыми эффекты взаимодействия и квадратичные эффекты. Близость «почти стационарной» области можно установить, если поставить дополнительные опыты в центре плана (x1 = 0, x2= 0, ..., xk = 0) и вычислить среднее 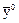 . Величина
. Величина 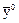 является оценкой для свободного члена уравнения теоретической регрессии:
является оценкой для свободного члена уравнения теоретической регрессии: 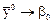 ,в то время как b0, подсчитываемый в факторном эксперименте по формуле
,в то время как b0, подсчитываемый в факторном эксперименте по формуле
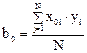
является совместной оценкой для свободного члена и суммы квадратичных членов
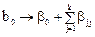
если теоретическое уравнение, регрессии представляет собой полином второго порядка. Поэтому разность
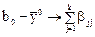
может до некоторой степени служить мерой кривизны поверхности.
Почти стационарную область описывают нелинейными - уравнениями.
В настоящее время достаточно разработаны планы только для полиномов второго порядка. Кроме того, поверхности второго порядка легко поддаются систематизации. Для описания поверхности отклика полиномами второй степени независимые факторы в планах должны принимать не менее трех разных значений.
Полный факторный эксперимент 3к содержит слишком большое число опытов.
Сократить число опытов можно, если воспользоваться так называемыми композиционными, или последовательными планами, предложенными Боксом и Уилсоном. «Ядро» таких планов составляет ПФЭ 2к при k < 5 или дробная реплика от него при k ≥ 5. Если линейное уравнение регрессии оказалось неадекватным, необходимо:
1) добавить 2 k «звездных» точек, расположенных на координатных осях факторного пространства (±α, 0, ..., 0), (0,± α, О, ..., 0), ..., (0,0, ..., О, ± α), где а—расстояние от центра плана до «звездной» точки — «звездное» плечо;
2) увеличить число экспериментов в центре плана n0. Общее число опытов в матрице композиционного плана при k факторах составит:
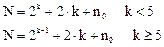
Рассмотрим построение композиционных планов на примере k=2. Точки 1,2,3,4 образуют ПФЭ 22, точки 5, 6, 7, 8 — «звездные» точки с координатами (±α, 0) и (0, ±α), координаты n0 опытов в центре плана нулевые (0,0).
Величина звездного плеча а и количество опытов в центре плана по зависят от выбранного плана.
Ортогональные планы второго порядка.
Композиционные планы легко приводятся к ортогональным выбором звездного плеча α. На количество опытов в центре плана по при этом не накладывается никаких ограничений. В этом случае n0 обычно принимают равным единице.
Возьмем матрицу композиционного планирования для k = 2, положив n0=1.
| N | х0 | х1 | х2 | х1 х2 | х12 | х22 |
| +1 | +1 | +1 | +1 | +1 | +1 | |
| +1 | +1 | -1 | -1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | +1 | +1 | |
| +1 | -1 | +1 | -1 | +1 | +1 | |
| +1 | +α | α2 | ||||
| +1 | -α | α2 | ||||
| +1 | +α | α2 | ||||
| +1 | -α | α2 | ||||
| +1 |
В общем виде приведенная матрица неортогональна, так как:
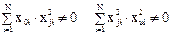
Приведем матрицу к ортогональному виду. Для этого преобразуем квадратичные переменные:
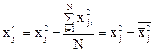
При этом
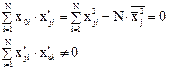
Чтобы сделать матрицу планирования полностью ортогональной, величину звездного плеча α выбирают из условия равенства нулю недиагонального члена корреляционной матрицы (Х*Х)-1.
| Число независимых факторов k | ||||
| “Ядро” плана | 22 | 23 | 24 | 25-1 |
| α | 1,00 | 1,215 | 1,414 | x5= x1 x2 x3 x4 1,547 |
В таблице приведены значения α для различного числа факторов.
Ортогональная матрица 2-го порядка для k = 2 имеет вид таблицы:
| N | х0 | х1 | х2 | х1 х2 | х12 | х22 |
| +1 | +1 | +1 | +1 | +1/3 | +1/3 | |
| +1 | +1 | -1 | -1 | +1/3 | +1/3 | |
| +1 | -1 | -1 | +1 | +1/3 | +1/3 | |
| +1 | -1 | +1 | -1 | +1/3 | +1/3 | |
| +1 | +1 | +1/3 | -2/3 | |||
| +1 | -1 | +1/3 | -2/3 | |||
| +1 | +1 | -2/3 | +1/3 | |||
| +1 | -1 | -2/3 | +1/3 | |||
| +1 | -2/3 | -2/3 |
В силу ортогональности матрицы планирования все коэффициенты регрессии определяются независимо друг от друга по формуле:
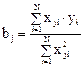
и дисперсии коэффициентов равны:
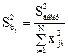
В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получим уравнение вида
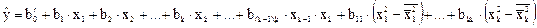
Чтобы перейти к обычной записи, определяют b0 по формуле:
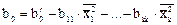
и оценивают с дисперсией, равной
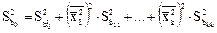
Зная дисперсию воспроизводимости, проверяют значимость коэффициентов и адекватность уравнения
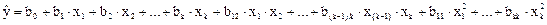
Адекватность уравнения проверяют по критерию Фишера, составляя отношение дисперсий F = Sост2/Sвоспр2 . Уравнение адекватно, если составленное таким образом F-отношение меньше табулированного для уровня значимости р (обычно равного 0,05) и чисел степеней свободы остаточной дисперсии и дисперсии воспроизводимости F < Fp(f1,f2), где f1 = N - l - число степеней свободы достаточной дисперсии; —число степеней свободы дисперсии воспроизводимости N—число опытов в матрице планирования; l—число коэффициентов в уравнении регрессии второго порядка.
Дата добавления: 2015-03-03; просмотров: 3238;
