Регрессионный анализ в матричной форме.

Регрессионный анализ в матричной форме удобен для решения задач на ЦВМ. Методом наименьших квадратов необходимо найти коэффициенты уравнения регрессии.

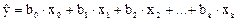
где x₀ — фиктивная переменная, равная 1.

Представим исходный статистический материал в матричной форме. Будем называть матрицу

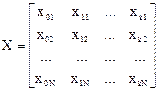
матрицей независимых переменных, а матрицу-столбец

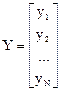
вектором наблюдений. Введем матрицу-столбец коэффициентов

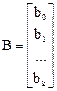
и матрицу, транспонированную к X:

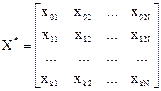
Система нормальных уравнений для определения b_o, b₁, ..., b_к имеет вид:

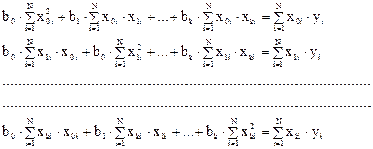
В матричной форме система нормальных уравнений запишется следующим образом:

X^* X B = X^* Y

Действительно, перемножив матрицы X* и X, имеем

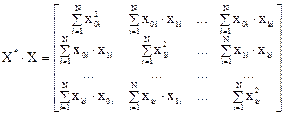
Умножив матрицу 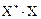на матрицу-столбец В, получим матрицу-столбец

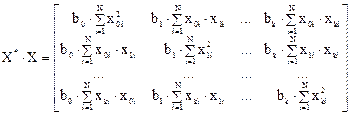
Умножив матрицу 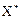на вектор наблюдений Y, получим:

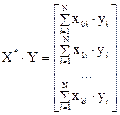
Из уравнения матрица-столбец коэффициентов В определяется следующим образом:

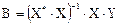
где (Х*Х)^-1—матрица, обратная матрице (Х*Х):

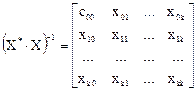
Элементы обратной матрицы определяются соотношением

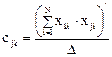или

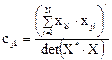
где det (Х*Х)илиΔ—определитель информационной матрицы Х*Х; 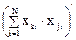— алгебраическое дополнение элемента 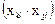в матрице Х*Х.

Для существования обратной матрицы (Х*Х)^-1 информационная матрица должна быть невырожденной. В связи с этим при использовании рассматриваемого вычислительного метода необходимо, чтобы переменные x₁, x₂, …, x_kбыли линейно независимыми. Тогда в матрице независимых переменных элементы одного столбца не будут линейной комбинацией соответствующих элементов других столбцов.

Необходимо заранее рассчитать выборочные коэффициенты корреляции между независимыми факторами. Если два фактора сильно коррелированы, один из них исключается из рассмотрения.