Метод множественной корреляции.
Если необходимо исследовать корреляционную связь между многими величинами, пользуются уравнениями множественной регрессии:

Здесь мы имеем дело уже не с линией регрессии, а с поверхностью регрессии при k = 2 и с гиперповерхностью при k > 2. В общем случае, как указывалось выше, эту поверхность называют поверхностью отклика.
При построении поверхности отклика на координатных осях факторного пространства откладываются численные значения параметров (факторов). Исходный статистический материал представляют в виде таблицы.
| № опыта | х1 | х2 | х3 | … | хк | y |
| х11 | х21 | х31 | хк1 | y1 | ||
| х12 | х22 | х32 | хк2 | y2 | ||
| х13 | х23 | х33 | хк3 | y3 | ||
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| N | х1N | х2N | х3N | хкN | yN |
Прежде всего перейдем от натурального масштаба к новому, проведя нормировку всех значений случайных величин по формулам:
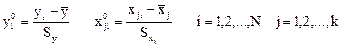
где у0i, хi0 — нормированные значения соответствующих факторов;
 - средние значения факторов; Sy, Sx,— среднеквадратичные отклонения факторов:
- средние значения факторов; Sy, Sx,— среднеквадратичные отклонения факторов:
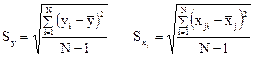
В таблице приведен исходный статистический материал в новом масштабе:
| № опыта | х10 | х20 | х30 | … | хк0 | y0 |
| х110 | х210 | х310 | хк10 | y10 | ||
| х120 | х220 | х320 | хк20 | y20 | ||
| х130 | х230 | х330 | хк30 | y30 | ||
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| N | х1N0 | х2N0 | х3N0 | хкN0 | yN0 |
В новом масштабе имеем:
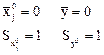
Выборочный коэффициент корреляции при этом равен:
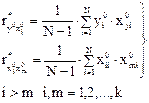
Вычисленный по формуле выборочный коэффициент корреляции равен коэффициенту корреляции между переменными, выраженными в натуральном масштабе r*ух.
Уравнение регрессии между нормированными переменными не имеет свободного члена и принимает вид:
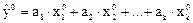
Коэффициенты уравнения находятся из условия:
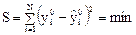
Условия минимума функции S определяются так же, как в случае зависимости от одной переменной:
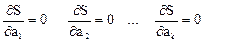
и система нормальных уравнений имеет вид:
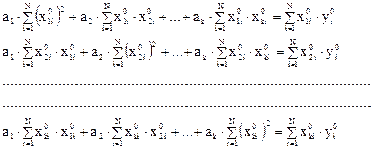
Умножим левую и правую части уравнений на 1/(N—1). В результате при каждом коэффициенте а, получается, согласно формуле, выборочный коэффициент корреляции r*. Принимая во внимание, что
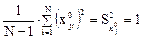
получаем систему нормальных уравнений:

Следует иметь в виду, что r* xl xm = r* xm xl . Коэффициенты корреляции легко вычисляются простым перемножением соответствующих столбцов таблицы. Для многопараметрических процессов система оказывается высокого порядка и для ее решения необходимо использовать вычислительную машину.
Решив систему, рассчитывают коэффициент множественной корреляции
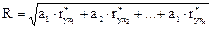
Коэффициент множественной корреляции служит показателем силы связи в случае множественной регрессии:
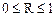
В случае выборок небольшого объема в величину R необходимо внести коррекцию на систематическую ошибку. Чем меньше число степеней свободы выборки f = N—l, тем сильнее преувеличивается сила связи, оцениваемая коэффициентом множественной корреляции. Формула для коррекции:
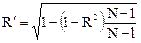
где R'—скорректированное значение коэффициента множественной корреляции; l—число коэффициентов уравнения регрессии.
Для практического использования уравнения необходимо перейти к натуральному масштабу по формулам:
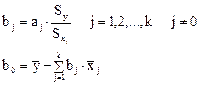
При наличии параллельных опытов можно рассчитать дисперсию воспроизводимости и провести статистический анализ уравнения регрессии.
Дата добавления: 2015-03-03; просмотров: 1851;
