Основные определения метода регрессионного анализа.

Для проведения регрессионного анализа необходимо выполнение следующих условий:

1. Входной параметр х измеряется с пренебрежимо малой ошибкой. Появление ошибки в определении у объясняется наличием в процессе невыявленных переменных, не вошедших в уравнение регрессии.

2. Результаты наблюдений над выходными величинами у₁, у₂ ,у₃ ,у_N представляют собой независимые нормально распределенные случайные величины.

3. При проведении эксперимента с объемом выборки N при условии, что каждый опыт повторен т раз, выборочные дисперсии S₁², S₂², ..., S_N² должны быть однородны.

Определение однородности дисперсий сводится к следующему;

1. Определяется среднее из результатов параллельных опытов;

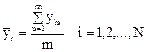
2. Определяются выборочные дисперсии:

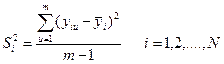
3. Находится сумма дисперсий:

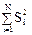
4. Составляется отношение:

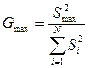
где S²_max - максимальное значение выборочной дисперсии. Если дисперсии однородны, то G_max<G_p(N, т-1), где G_p(N, m-1)-табулированное значение критерия Кохрена при уровне значимости р.

Если выборочные дисперсии однородны, рассчитывается дисперсия воспроизводимости:

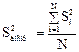
Число степеней свободы этой дисперсии f равно:

f=N (m-1)

Дисперсия воспроизводимости необходима для оценки значимости коэффициентов уравнения регрессии. Оценка значимости коэффициентов производится по критерию Стьюдента:

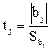
где b_j - j-ый коэффициент уравнения регрессии; S_bj - среднее квадратичное отклонение j-го коэффициента.

Если t_j больше табулированного t_p(f) для выбранного уровня значимости р и числа степеней свободы f, то коэффициент b_j, значимо отличается от нуля; S_bj определяется по закону накопления ошибок:

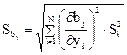
Если S₁² = S²₂=…=S_N²=S²_воспр, получим:

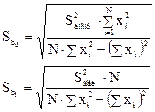
Незначимые коэффициенты исключаются из уравнения регрессии. Оставшиеся коэффициенты пересчитываются заново поскольку коэффициенты закоррелированы друг с другом. Адекватность уравнения проверяется по критерию Фишера:

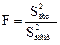
где S²_воспр — дисперсия воспроизводимости; S²_ост — остаточная дисперсия

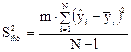
Если отношение меньше табличного F_p(f₁, f₂), уравнение адекватно.

При отсутствии параллельных опытов и дисперсии воспроизводимости можно оценить качество аппроксимации принятым уравнением, сравнив S²_ост и дисперсию относительно среднего S²_у

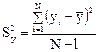
по критерию Фишера

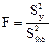
В этом случае критерий Фишера показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное F_p(f₁, f₂) для выбранного уровня значимости р и чисел степеней свободы f₁ = N—1 и f₂ = N—l, тем эффективнее уравнение регрессии.